
科目: 来源: 题型:
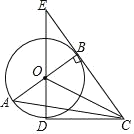
【题目】如图,AB是⊙O的直径,过点B做⊙O的切线BC,点D为⊙O上一点,且CD=CB,连结DO并延长交CB的延长线于点E.
(1)求证:CD是⊙O的切线;
(2)连接AC,若BE=4,DE=8,求线段AC的长.
查看答案和解析>>
科目: 来源: 题型:
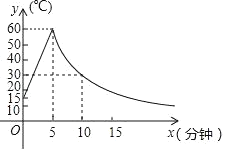
【题目】工厂对某种新型材料进行加工,首先要将其加温,使这种材料保持在一定温度范围内方可加工,如图是在这种材料的加工过程中,该材料的温度y(℃)时间x(min)变化的数图象,已知该材料,初始温度为15℃,在温度上升阶段,y与x成一次函数关系,在第5分钟温度达到60℃后停止加温,在温度下降阶段,y与x成反比例关系.
(1)写出该材料温度上升和下降阶段,y与x的函数关系式:
①上升阶段:当0≤x≤5时,y= ;
②下降阶段:当x>5时,y .
(2)根据工艺要求,当材料的温度不低于30℃,可以进行产品加工,请问在图中所示的温度变化过程中,可以进行加工多长时间?
查看答案和解析>>
科目: 来源: 题型:
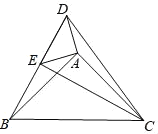
【题目】如图,点E在△DBC边DB上,点A在△DBC内部,∠DAE=∠BAC=90°,AD=AE,AB=AC.给出下列结论,其中正确的是_____(填序号)①BD⊥CE②∠DCB﹣∠ABD=45°③CE﹣BE=![]() AD④BE2+CD2=2(AD2+AB2)
AD④BE2+CD2=2(AD2+AB2)
查看答案和解析>>
科目: 来源: 题型:
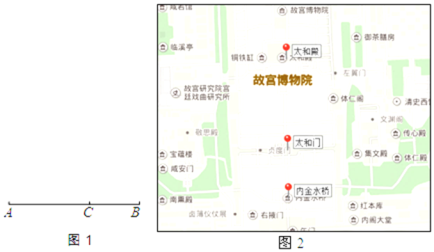
【题目】如图1,在线段AB上找一点C,C把AB分为AC和CB两段,其中BC是较小的一段,如果BCAB=AC2,那么称线段AB被点C黄金分割.为了增加美感,黄金分割经常被应用在绘画、雕塑、音乐、建筑等艺术领域.如图2,在“附中博识课程中”,小白菜们沿着紫禁城的中轴线,从内金水桥走到了太和殿,领略了古代建筑的宏伟.太和门位于太和殿与内金水桥之间靠近内金水桥的一侧,三个建筑的位置关系满足黄金分割.已知太和殿到内金水桥的距离约为100丈,设太和门到太和殿之间的距离为x丈,要求x,则可列方程为________________.
查看答案和解析>>
科目: 来源: 题型:
【题目】根据研究,人体内血乳酸浓度升高是运动后感觉疲劳的重要原因,运动员未运动时,体内血乳酸浓度水平通常在40mg/L以下;如果血乳酸浓度降到50mg/L以下,运动员就基本消除了疲劳,体育科研工作者根据实验数据,绘制了一副图象,它反映了运动员进行高强度运动后,体内血乳酸浓度随时间变化而变化的函数关系.下列叙述正确的是( )
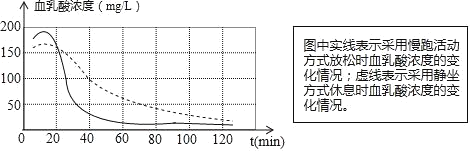
A. 运动后40min时,采用慢跑活动方式放松时的血乳酸浓度与采用静坐方式休息时的血乳酸浓度相同
B. 运动员高强度运动后,最高血乳酸浓度大约为250mg/L
C. 采用慢跑活动方式放松时,运动员必须慢跑70min后才能基本消除疲芳
D. 运动员进行完剧烈运动,为了更快达到消除疲劳的效果,应该采用慢跑活动方式来放松
查看答案和解析>>
科目: 来源: 题型:
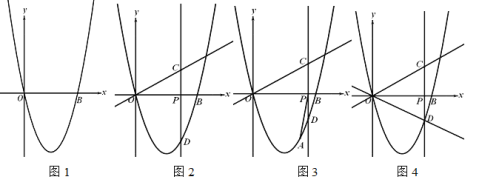
【题目】已知,二次函数![]() 的图像与x轴的一个交点为O(0,0),点P(m,0)是x轴正半轴上的一个动点.
的图像与x轴的一个交点为O(0,0),点P(m,0)是x轴正半轴上的一个动点.
(1)如图1,求二次函数的图像与x轴另一个交点的坐标;
(2)如图2,过点P作x轴的垂线交直线![]() 与点C,交二次函数图像于点D,
与点C,交二次函数图像于点D,
①当PD=2PC时,求m的值;
如图3,已知A(3,-3)在二次函数图像上,连结AP,求![]() 的最小值;
的最小值;
(3如图4,在第(2)小题的基础上,作直线OD,作点C关于直线OD的对称点C’,当C’落在坐标轴上时,请直接写出m的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】中秋节期间,大润发超市将购进一批月饼进行销售,已知购进4盒甲品牌月饼和6盒乙品牌月饼需260元,购进5盒甲品牌月饼和4盒乙品牌月饼需220元.甲乙两种品牌月饼以相同的售价销售,甲品牌月饼的销量![]() (盒)与售价
(盒)与售价![]() (元)之间的关系为
(元)之间的关系为![]() ;当售价为40元时,乙品牌月饼可销售100盒,售价每提高1元,少销售5盒.
;当售价为40元时,乙品牌月饼可销售100盒,售价每提高1元,少销售5盒.
(1)求甲乙两种品牌月饼每盒的进价分别为多少元?
(2)当乙品牌月饼的售价为多少元时,乙品牌月饼的销售总利润最大?此时甲乙两种品牌月饼的销售总利润为多少?
(3)当甲品牌月饼的销售量不低乙品牌月饼的销售量的![]() ,若使两种品牌月饼的总利润最高,求此时的定价为多少?
,若使两种品牌月饼的总利润最高,求此时的定价为多少?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图所示,M为等腰三角形ABD的底边AB的中点,过D作DC∥AB,连接BC,AB=6cm,DM=3cm,DC=3-![]() cm.动点P自A点出发,在AB上匀速运动,动点Q自点B出发,在折线BC-CD上匀速运动,速度均为1cm/s,两点同时出发,当其中一个动点到达终点时,它们同时停止运动,设点P运动t(s)时,△MPQ的面积为S.
cm.动点P自A点出发,在AB上匀速运动,动点Q自点B出发,在折线BC-CD上匀速运动,速度均为1cm/s,两点同时出发,当其中一个动点到达终点时,它们同时停止运动,设点P运动t(s)时,△MPQ的面积为S.
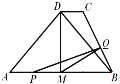
(1)当点P在线段AM上运动时,PM=_______.(用t的代数式表示)
(2)求BC的长度;
(3)当点P在MB上运动时,求S与t之间的函数关系式.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,AB∥CD,连结AD,点E是AD的中点,连结BE并延长交CD于F点.
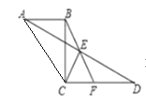
(1)请说明△ABE≌△DFE的理由;
(2)连结CE,AC,若CB⊥CD,AC=CD,∠D=30°,CD=2,求BF的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com