
科目: 来源: 题型:
【题目】如图,△ABC中,∠ACB=90°,sinA=![]() ,BC=8,点D是AB的中点,过点B作CD的垂线,垂足为点E.
,BC=8,点D是AB的中点,过点B作CD的垂线,垂足为点E.
(1)求线段CD的长;
(2)求cos∠ABE的值。

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,四边形ABCD内接于⊙O,AB=AD,对角线BD为⊙O的直径,AC与BD交于点E.点F为CD延长线上,且DF=BC.
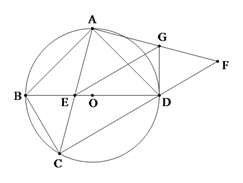
(1)证明:AC=AF;
(2)若AD=2,AF=![]() ,求AE的长;
,求AE的长;
(3)若EG∥CF交AF于点G,连接DG.证明:DG为⊙O的切线.
查看答案和解析>>
科目: 来源: 题型:
【题目】抛物线y=ax2+bx+c的对称轴为直线x=﹣1,部分图象如图所示,下列判断中:
①4ac<b2;
②a>b>c;
③一次函数y=ax+c的图象不经第四象限;
④m(am+b)+b<a(m是任意实数);
⑤3b+2c>0.
其中正确的个数是( )
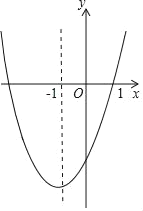
A.1B.2C.3D.4
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,有A、B两个转盘,其中转盘A被分成4等份,转盘B被分成3等份,并在每一份内标上数字。现甲、乙两人同时各转动其中一个转盘,转盘停止后(当指针指在边界线上时视为无效,重转),若将A转盘指针指向的数字记为x,B转盘指针指向的数字记为y,从而确定点P的坐标为P(x,y);记S=x+y。
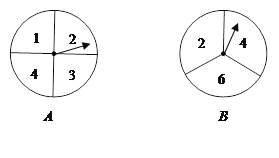
【1】请用列表或画树状图的方法写出所有可能得到的点P的坐标;
【2】李刚为甲、乙两人设计了一个游戏:当S<6时甲获胜,否则乙获胜。你认为这个游戏公平吗?对谁有利?
查看答案和解析>>
科目: 来源: 题型:
【题目】甲、乙两人进行羽毛球比赛,羽毛球飞行的路线为抛物线的一部分,如图,甲在![]() 点上正方
点上正方![]() 的
的![]() 处发出一球,羽毛球飞行的高度
处发出一球,羽毛球飞行的高度![]() 与水平距离
与水平距离![]() 之间满足函数表达式
之间满足函数表达式![]() .已知点
.已知点![]() 与球网的水平距离为
与球网的水平距离为![]() ,球网的高度为
,球网的高度为![]() .
.
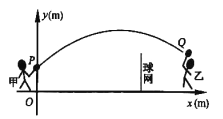
(1)当![]() 时,①求
时,①求![]() 的值.②通过计算判断此球能否过网.
的值.②通过计算判断此球能否过网.
(2)若甲发球过网后,羽毛球飞行到点![]() 的水平距离为
的水平距离为![]() ,离地面的高度为
,离地面的高度为![]() 的
的![]() 处时,乙扣球成功,求
处时,乙扣球成功,求![]() 的值.
的值.
查看答案和解析>>
科目: 来源: 题型:
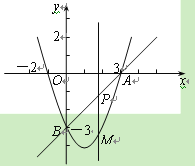
【题目】如图,在平面直角坐标系中,抛物线y=x2+mx+n经过点A(3,0)、
B(0,-3),点P是直线AB上的动点,过点P作x轴的垂线交抛物线于点M,设点P的横
坐标为t.
(1)分别求出直线AB和这条抛物线的解析式.
(2)若点P在第四象限,连接AM、BM,当线段PM最长时,求△ABM的面积.
(3)是否存在这样的点P,使得以点P、M、B、O为顶点的四边形为平行四边形?若存在,请直接写出点P的横坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】抛物线![]() 与y轴交于点
与y轴交于点![]() .
.
(1)求抛物线的解析式;
(2)求抛物线与坐标轴的交点坐标;
(3)①当x取什么值时, ![]() ?
? ![]() 当x取什么值时,y的值随x的增大而减小?
当x取什么值时,y的值随x的增大而减小?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图所示是二次函数![]() 图象的一部分,图象过点
图象的一部分,图象过点![]() ,二次函数图象对称轴为直线
,二次函数图象对称轴为直线![]() ,给出五个结论:①
,给出五个结论:①![]() ;②
;②![]() ;③当
;③当![]() 时,
时,![]() 随
随![]() 的增大而增大;④方程
的增大而增大;④方程![]() 的根为
的根为![]() ,
,![]() ;⑤
;⑤![]() 其中正确结论是( )
其中正确结论是( )

A. ①②③ B. ①③④ C. ②③④ D. ③④⑤
查看答案和解析>>
科目: 来源: 题型:
【题目】如图所示,学校准备在教学楼后面搭建一个简易矩形自行车车棚,一边利用教学楼的后墙(可利用的墙长为19m),另外三边利用学校现有总长38m的铁栏围成.
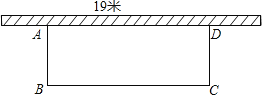
(1)若围成的面积为180m,试求出自行车车棚的长和宽;
(2)能围成的面积为200m自行车车棚吗?如果能,请你给出设计方案;如果不能,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com