
科目: 来源: 题型:
【题目】如图,抛物线y=x2+bx+c与直线y=![]() x﹣3交于,B两点,其中点A在y轴上,点B坐标为(﹣4,﹣5),点P为y轴左侧的抛物线上一动点,过点P作PC⊥x轴于点C,交AB于点D.
x﹣3交于,B两点,其中点A在y轴上,点B坐标为(﹣4,﹣5),点P为y轴左侧的抛物线上一动点,过点P作PC⊥x轴于点C,交AB于点D.
(1)求抛物线对应的函数解析式;
(2)以O,A,P,D为顶点的平行四边形是否存在若存在,求点P的坐标;若不存在,说明理由.

查看答案和解析>>
科目: 来源: 题型:
【题目】请你利用直角坐标平面上任意两点(x1,y1)、(x2,y2)间的距离公式![]() 解答下列问题:
解答下列问题:
已知:反比例函数![]() 与正比例函数y=x的图象交于A、B两点(A在第一象限),点F1(﹣2,﹣2)、F2(2,2)在直线y=x上.设点P(x0,y0)是反比例函数
与正比例函数y=x的图象交于A、B两点(A在第一象限),点F1(﹣2,﹣2)、F2(2,2)在直线y=x上.设点P(x0,y0)是反比例函数![]() 图象上的任意一点,记点P与F1、F2两点的距离之差d=|PF1﹣PF2|.试比较线段AB的长度与d的大小,并由此归纳出双曲线的一个重要定义(用简练的语言表述).
图象上的任意一点,记点P与F1、F2两点的距离之差d=|PF1﹣PF2|.试比较线段AB的长度与d的大小,并由此归纳出双曲线的一个重要定义(用简练的语言表述).
查看答案和解析>>
科目: 来源: 题型:
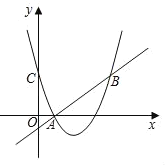
【题目】如图,二次函数y=(x﹣3)2+m的图象与y轴交于点C,点B是点C关于该二次函数图象的对称轴对称的点,已知一次函数y=kx+b的图象经过该二次函数图象上的点A(1,0)及点B.
(1)求二次函数与一次函数的解析式;
(2)抛物线上是否存在一点P,使S△ABP=S△ABC?若存在,请求出点P的坐标,若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】有一个二次函数满足以下条件:
①函数图象与x轴的交点坐标分别为A(1,0),B(x2,y2)(点B在点A的右侧);
②对称轴是x=3;
③该函数有最小值是﹣2.
(1)请根据以上信息求出二次函数表达式;
(2)将该函数图象x>x2的部分图象向下翻折与原图象未翻折的部分组成图象“G”,平行于x轴的直线与图象“G”相交于点C(x3,y3)、D(x4,y4)、E(x5,y5)(x3<x4<x5),结合画出的函数图象求x3+x4+x5的取值范围.

查看答案和解析>>
科目: 来源: 题型:
【题目】抛物线y=ax2+bx+3(a≠0)过A(4,4),B(2,m)两点,点B到抛物线对称轴的距离记为d,满足0<d≤1,则实数m的取值范围是( )
A. m≤2或m≥3 B. m≤3或m≥4 C. 2<m<3 D. 3<m<4
查看答案和解析>>
科目: 来源: 题型:
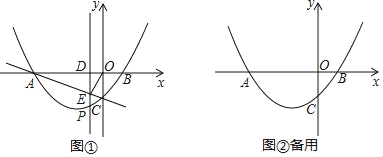
【题目】如图,抛物线y=![]() 与x轴分别交于A、B两点(点A在点B的左侧,)与y轴交于点C,作直线AC.
与x轴分别交于A、B两点(点A在点B的左侧,)与y轴交于点C,作直线AC.
(1)点B的坐标为 ,直线AC的关系式为 .
(2)设在直线AC下方的抛物线上有一动点P,过点P作PD⊥x轴于D,交直线AC于点E,当CE平分∠OEP时求点P的坐标.
(3)点M在x轴上,点N在抛物线上,试问以点A、C、M、N为顶点的四边形能否成为平行四边形?若存在,直接写出所有点M的坐标;若不存在,请简述你的理由.
查看答案和解析>>
科目: 来源: 题型:
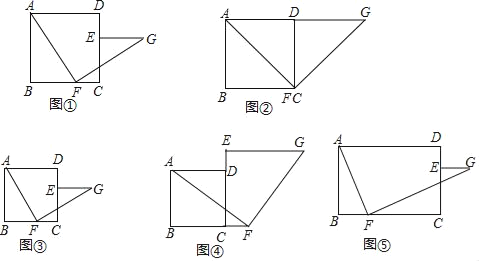
【题目】(综合与实践)如图①,在正方形ABCD中,点E、F分别在射线CD、BC上,且BF=CE,将线段FA绕点F顺时针旋转90°得到线段FG,连接EG,试探究线段EG和BF的数量关系和位置关系.
(观察与猜想)任务一:“智慧小组”首先考虑点E、F的特殊位置如图②,当点E与点D重合,点F与点C重合时,易知:EG与BF的数量关系是 ,EG与BF的位置关系是 .
(探究与证明)任务二:“博学小组”同学认为E、F不一定必须在特殊位置,他们分两种情况,一种是点E、F分别在CD、BC边上任意位置时(如图③);一种是点E、F在CD、BC边的延长线上的任意位置时(如图④),线段EG与BF的数量关系与位置关系仍然成立.请你选择其中一种情况给出证明.
(拓展与延伸)“创新小组”同学认为,若将“正方形ABCD”改为“矩形ABCD,且![]() =k(k≠1)”,点E、F分别在射线CD、BC上任意位置时,仍将线段FA绕点F顺时针旋转90°,并适当延长得到线段FG,连接EG(如图⑤),则当线段BF、CE、AF、FG满足一个条件 时,线段EG与BF的数量关系与位置关系仍然成立.(请你在横线上直接写出这个条件,无需证明)
=k(k≠1)”,点E、F分别在射线CD、BC上任意位置时,仍将线段FA绕点F顺时针旋转90°,并适当延长得到线段FG,连接EG(如图⑤),则当线段BF、CE、AF、FG满足一个条件 时,线段EG与BF的数量关系与位置关系仍然成立.(请你在横线上直接写出这个条件,无需证明)
查看答案和解析>>
科目: 来源: 题型:
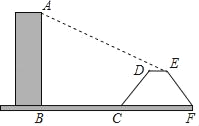
【题目】如图,AB是垂直于水平面的一座大楼,离大楼20米(BC=20米)远的地方有一段斜坡CD(坡度为1:0.75),且坡长CD=10米,某日下午一个时刻,在太阳光照射下,大楼的影子落在了水平面BC,斜坡CD,以及坡顶上的水平面DE处(A、B、C、D、E均在同一个平面内).若DE=4米,且此时太阳光与水平面所夹锐角为24°(∠AED=24°),试求出大楼AB的高.(其中,sin24°≈0.41,cos24°≈0.91,tan24°≈0.45)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com