
科目: 来源: 题型:
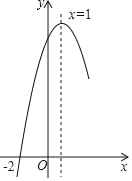
【题目】抛物线y=ax2+bx+c经过点(﹣2,0),且对称轴为直线x=1,其部分图象如图所示.对于此抛物线有如下四个结论:
①ac>0;②16a+4b+c=0;③若m>n>0,则x=1+m时的函数值大于x=1﹣n时的函数值;④点(﹣![]() ,0)一定在此抛物线上.其中正确结论的序号是( )
,0)一定在此抛物线上.其中正确结论的序号是( )
A. ①②B. ②③C. ②④D. ③④
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 的的顶点为
的的顶点为![]() .
.
(1)顶点![]() 的坐标为 .
的坐标为 .
(2)横、纵坐标都是整数的点叫做整点.若![]()
![]() 轴且
轴且![]()
①点![]() 的坐标为 ;
的坐标为 ;
②过点![]() 作
作![]() 轴的垂线
轴的垂线![]() ,若直线
,若直线![]() 与抛物线交于
与抛物线交于![]() 两点,该抛物线在
两点,该抛物线在![]() 之间的部分与线段
之间的部分与线段![]() 所围成的区域(包括边界)恰有七个整点,结合函数图象,求
所围成的区域(包括边界)恰有七个整点,结合函数图象,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知某种汽车刹车后行驶的距离s(单位:m)关于行驶的时间t(单位:s)的函数关系式为s=15t-at2,且t=1时,s=9.
(1)求s与t的函数关系式;
(2)该汽车刹车后到停下来前进了多远?
(3)该汽车刹车后前进6m时行驶了多长时间?
查看答案和解析>>
科目: 来源: 题型:
【题目】已知:直线y=ax+b与抛物线![]() 的一个交点为(0,2),同时这条直线与x轴相交于点A,且相交所成的角为45°.
的一个交点为(0,2),同时这条直线与x轴相交于点A,且相交所成的角为45°.
(1)点A的坐标为__________;
(2)若抛物线![]() 与x轴交于点M、N(点M在点N左边),将此抛物线作关于y轴对称,M的对应点为E,两抛物线相交于点F,连接NF,EF得△NEF,P是轴对称后的抛物线上的点,使得△NEP的面积与△NEF的面积相等,则P点坐标为_________.
与x轴交于点M、N(点M在点N左边),将此抛物线作关于y轴对称,M的对应点为E,两抛物线相交于点F,连接NF,EF得△NEF,P是轴对称后的抛物线上的点,使得△NEP的面积与△NEF的面积相等,则P点坐标为_________.

查看答案和解析>>
科目: 来源: 题型:
【题目】某超市销售一种文具,进价为5元/件.售价为6元/件时,当天的销售量为100件.在销售过程中发现:售价每上涨0.5元,当天的销售量就减少5件.设当天销售单价统一为![]() 元/件(
元/件(![]() ,且
,且![]() 是按0.5元的倍数上涨),当天销售利润为
是按0.5元的倍数上涨),当天销售利润为![]() 元.
元.
(1)求![]() 与
与![]() 的函数关系式(不要求写出自变量的取值范围);
的函数关系式(不要求写出自变量的取值范围);
(2)要使当天销售利润不低于240元,求当天销售单价所在的范围;
(3)若每件文具的利润不超过![]() ,要想当天获得利润最大,每件文具售价为多少元?并求出最大利润.
,要想当天获得利润最大,每件文具售价为多少元?并求出最大利润.
查看答案和解析>>
科目: 来源: 题型:
【题目】为纪念建国70周年,某校举行班级歌咏比赛,歌曲有:《我爱你,中国》,《歌唱祖国》,《我和我的祖国》(分别用字母A,B,C依次表示这三首歌曲).比赛时,将A,B,C这三个字母分别写在3张无差别不透明的卡片正面上,洗匀后正面向下放在桌面上,八(1)班班长先从中随机抽取一张卡片,放回后洗匀,再由八(2)班班长从中随机抽取一张卡片,进行歌咏比赛.
(1)八(1)班抽中歌曲《我和我的祖国》的概率是__________;
(2)试用画树状图或列表的方法表示所有可能的结果,并求出八(1)班和八(2)班抽中不同歌曲的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系![]() 中,抛物线y=x2-4x+3与x轴交于点A 、B(点A在点B的左侧),与y轴交于点C.
中,抛物线y=x2-4x+3与x轴交于点A 、B(点A在点B的左侧),与y轴交于点C.
(1)求直线BC的表达式;
(2)垂直于y轴的直线l与抛物线交于点![]() ,与直线BC交于点
,与直线BC交于点![]() ,若x1<x2<x3,结合函数的图象,求x1+x2+x3的取值范围.
,若x1<x2<x3,结合函数的图象,求x1+x2+x3的取值范围.
查看答案和解析>>
科目: 来源: 题型:
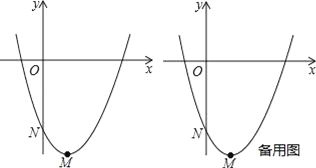
【题目】已知抛物线l:y=ax2+bx+c(a,b,c均不为0)的顶点为M,与y轴的交点为N,我们称以N为顶点,对称轴是y轴且过点M的抛物线为抛物线l的衍生抛物线,直线MN为抛物线l的衍生直线.
(1)如图,抛物线y=x2﹣2x﹣3的衍生抛物线的解析式是 ,衍生直线的解析式是 ;
(2)若一条抛物线的衍生抛物线和衍生直线分别是y=﹣2x2+1和y=﹣2x+1,求这条抛物线的解析式;
(3)如图,设(1)中的抛物线y=x2﹣2x﹣3的顶点为M,与y轴交点为N,将它的衍生直线MN先绕点N旋转到与x轴平行,再沿y轴向上平移1个单位得直线n,P是直线n上的动点,是否存在点P,使△POM为直角三角形?若存在,求出所有点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】“校园安全”受到全社会的广泛关注,东营市某中学对部分学生就校园安全知识的了解程度,采用随机抽样调查的方式,并根据收集到的信息进行统计,绘制了下面两幅尚不完整的统计图.请你根据统计图中所提供的信息解答下列问题:

(1)接受问卷调查的学生共有_______人,扇形统计图中“基本了解”部分所对应扇形的圆心角为_______°;
(2)请补全条形统计图;
(3)若该中学共有学生900人,请根据上述调查结果,估计该中学学生中对校园安全知识达到“了解”和“基本了解”程度的总人数;
(4)若从对校园安全知识达到“了解”程度的3个女生和2个男生中随机抽取2人参加校园安全知识竞赛,请用树状图或列表法求出恰好抽到1个男生和1个女生的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com