
科目: 来源: 题型:
【题目】如图,是一座古拱桥的截面图,拱桥桥洞的上沿是抛物线形状,当水面的宽度为10m时,桥洞与水面
的最大距离是5m.
(1)经过讨论,同学们得出三种建立平面直角坐标系的方案(如下图)
你选择的方案是_____(填方案一,方案二,或方案三),则B点坐标是______,求出你所选方案中的抛物线的表达式;
(2)因为上游水库泄洪,水面宽度变为6m,求水面上涨的高度.


查看答案和解析>>
科目: 来源: 题型:
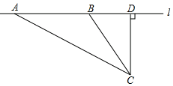
【题目】校车安全是近几年社会关注的重大问题,安全隐患主要是超速和超载,某中学数学活动小组设计了如下检测公路上行驶的汽车速度的实验:先在公路旁边选取一点C,再在笔直的车道l上确定点D,使CD与l垂直,测得CD的长等于24米,在l上点D的同侧取点A、B,使∠CAD=30°,∠CBD=60°.
(1)求AB的长(结果保留根号);
(2)已知本路段对校车限速为45千米/小时,若测得某辆校车从A到B用时1.5秒,这辆校车是否超速?说明理由.(参考数据:![]() ≈1.7,
≈1.7,![]() ≈1.4)
≈1.4)
查看答案和解析>>
科目: 来源: 题型:
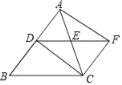
【题目】如图,DE是△ABC的中位线,过点C作CF∥BD交DE的延长线于点F,连接AF、DC.
(1)求证:四边形ADCF是平行四边形;
(2)若AC=BC,判断四边形ADCF的形状,无需说明理由;
(3)若∠ACB=90°,判断四边形ADCF的形状,无需说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】某校随机抽取九年级部分同学接受一次内容为“最适合自己的考前减压方式”的调查活动,学校收集整理数据后,将减压方式分为五类,并绘制了图1、图2两个不完整的统计图,请根据图中的信息解答下列问题:
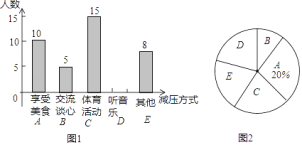
![]() 九年级接受调查的同学共有多少名,并补全条形统计图;
九年级接受调查的同学共有多少名,并补全条形统计图;
![]() 九年级共有500名学生,请你估计该校九年级听音乐减压的学生有多少名;
九年级共有500名学生,请你估计该校九年级听音乐减压的学生有多少名;
![]() 若喜欢“交流谈心”的5名同学中有三名男生和两名女生,心理老师想从5名同学中任选两名同学进行交流,请用画树状图或列表的方法求同时选出的两名同学都是女生的概率.
若喜欢“交流谈心”的5名同学中有三名男生和两名女生,心理老师想从5名同学中任选两名同学进行交流,请用画树状图或列表的方法求同时选出的两名同学都是女生的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知直线l:y=﹣x+4,在直线l上取点B1,过B1分别向x轴,y轴作垂线,交x轴于A1,交y轴于C1,使四边形OA1B1C1为正方形;在直线l上取点B2,过B2分别向x轴,A1B1作垂线,交x轴于A2,交A1B1于C2,使四边形A1A2B2C2为正方形;按此方法在直线l上顺次取点B3,B4,…,Bn,依次作正方形A2A3B3C3,A3A4B4C4,…,An﹣1AnBnCn,则A3的坐标为___,B5的坐标为___.

查看答案和解析>>
科目: 来源: 题型:
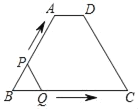
【题目】如图,在四边形ABCD中,AD∥BC,AB=CD,∠B=60°,AD=2,BC=8,点P从点B出发沿折线BA﹣AD﹣DC匀速运动,同时,点Q从点B出发沿折线BC﹣CD匀速运动,点P与点Q的速度相同,当二者相遇时,运动停止,设点P运动的路程为x,△BPQ的面积为y,则y关于x的函数图象大致是( )
A.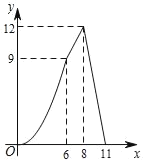 B.
B.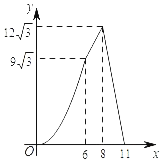
C.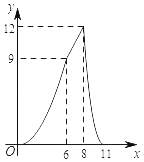 D.
D.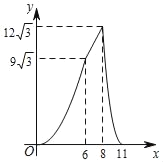
查看答案和解析>>
科目: 来源: 题型:
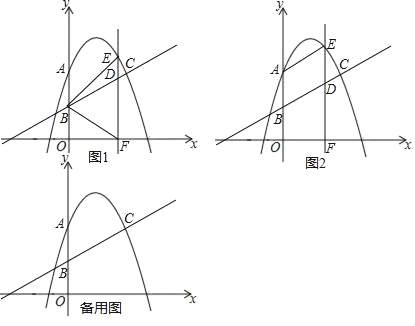
【题目】如图,抛物线y=﹣x2+bx+c经过A(0,3),C(2,n)两点,直线l:y=![]() x+2过C点,且与y轴交于点B,抛物线上有一动点E,过点E作直线EF⊥x轴于点F,交直线BC于点D
x+2过C点,且与y轴交于点B,抛物线上有一动点E,过点E作直线EF⊥x轴于点F,交直线BC于点D
(1)求抛物线的解析式.
(2)如图1,当点E在直线BC上方的抛物线上运动时,连接BE,BF,是否存在点E使直线BC将△BEF的面积分为2:3两部分?若存在,求出点E的坐标,若不存在说明理由;
(3)如图2,若点E在y轴右侧的抛物线上运动,连接AE,当∠AED=∠ABC时,直接写出此时点E的坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图1,已知直角三角形ABC,∠ACB=90°,∠BAC=30°,点D是AC边上一点,过D作DE⊥AB于点E,连接BD,点F是BD中点,连接EF,CF.
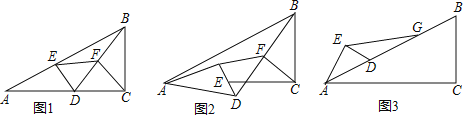
(1)发现问题:线段EF,CF之间的数量关系为_____;∠EFC的度数为_____;
(2)拓展与探究:若将△AED绕点A按顺时针方向旋转α角(0°<α<30°),如图2所示,(1)中的结论还成立吗?请说明理由;
(3)拓展与运用:如图3所示,若△AED绕点A旋转的过程中,当点D落到AB边上时,AB边上另有一点G,AD=DG=GB,BC=3,连接EG,请直接写出EG的长度.
查看答案和解析>>
科目: 来源: 题型:
【题目】“莓好河南,幸福家园”,2019年某省草莓旅游文化节期间,甲、乙两家草莓采摘园草莓品质相同,销售价格也相同,且推出了如下的优惠方案:
甲园 | 游客进园需购买20元/人的门票,采摘的草莓六折优惠 |
乙园 | 游客进园不需购买门票,采摘的草莓超过一定数量后,超过部分打折优惠 |
活动期间,小雪与爸爸妈妈决定选一个周末一同去采摘草莓,若设他们的草莓采摘量为x(千克)(出园时欲将自己采摘的草莓全部购买),在甲采摘园所需总费用为y1(元),在乙采摘园所需总费用为y2(元),图中折线OAB表示y2与x之间的函数关系.

(1)求y1、y2与x之间的函数关系式;
(2)请在图中画出y1与x之间大致的函数图象;
(3)若小雪和爸爸妈妈当天所采摘的草莓不少于10千克,则选择哪个草莓园更划算?请说明理由.
查看答案和解析>>
科目: 来源: 题型:
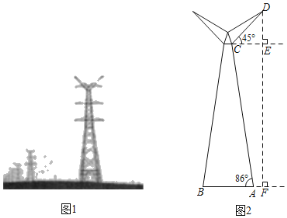
【题目】如图所示,图1,图2分别是某款高压电塔的实物图和示意图电塔的底座AB与地面平齐,DF表示电塔顶端D到地面的距离,已知AF的长是2米,支架AC与地面夹角∠BAC=86°,顶端支架DC长10米,DC与水平线CE之间夹角∠DCE=45°,求电塔的高度DF.(sin86°=0.998,cos86°=0.070,tan86°=14.300,![]() ≈1.4,结果保留整数)
≈1.4,结果保留整数)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com