
科目: 来源: 题型:
【题目】(1)问题发现
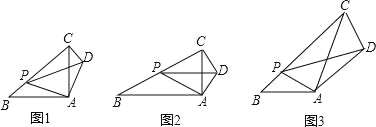
如图1,在Rt△ABC中,∠A=90°,![]() =1,点P是边BC上一动点(不与点B重合),∠PAD=90°,∠APD=∠B,连接 CD.
=1,点P是边BC上一动点(不与点B重合),∠PAD=90°,∠APD=∠B,连接 CD.
(1)①求![]() 的值;②求∠ACD的度数.
的值;②求∠ACD的度数.
(2)拓展探究
如图 2,在Rt△ABC中,∠A=90°,![]() =k.点P是边BC上一动点(不与点B重合),∠PAD=90°,∠APD=∠B,连接CD,请判断∠ACD与∠B 的数量关系以及PB与CD之间的数量关系,并说明理由.
=k.点P是边BC上一动点(不与点B重合),∠PAD=90°,∠APD=∠B,连接CD,请判断∠ACD与∠B 的数量关系以及PB与CD之间的数量关系,并说明理由.
(3)解决问题
如图 3,在△ABC中,∠B=45°,AB=4![]() ,BC=12,P 是边BC上一动点(不与点B重合),∠PAD=∠BAC,∠APD=∠B,连接CD.若 PA=5,请直接写出CD的长.
,BC=12,P 是边BC上一动点(不与点B重合),∠PAD=∠BAC,∠APD=∠B,连接CD.若 PA=5,请直接写出CD的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知:如图,在![]() 中,
中,![]() 分别是
分别是![]() 、
、![]() 的中点,
的中点,![]() 分别是对角线
分别是对角线![]() 上的四等分点,顺次连接
上的四等分点,顺次连接![]() .
.
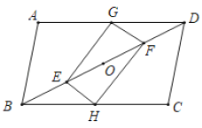
(1)求证:四边形![]() 是平行四边形;
是平行四边形;
(2)当![]() 满足____ 条件时,四边形
满足____ 条件时,四边形![]() 是菱形;
是菱形;
(3)若![]() ,
,
①探究四边形![]() 的形状,并说明理由;
的形状,并说明理由;
②当![]() 时,直接写出四边形
时,直接写出四边形![]() 的面积.
的面积.
查看答案和解析>>
科目: 来源: 题型:
【题目】某汽车租赁公司共有汽车50辆,市场调查表明,当租金为每辆每日200元时可全部租出,当租金每提高10元,租出去的车就减少2辆.
(1)当租金提高多少元时,公司的每日收益可达到10120元?
(2)公司领导希望日收益达到10200元,你认为能否实现?若能,求出此时的租金,若不能,请说明理由.
(3)汽车日常维护要一定费用,已知外租车辆每日维护费为100元,未租出的车辆维护费为50元,当租金为多少元时,公司的利润恰好为5500元?(利润=收益一维护费).
查看答案和解析>>
科目: 来源: 题型:
【题目】校园安全受到全社会的广泛关注,某市某中学对部分学生就校园安全知识的了解程度,采用随机抽样调查的方式,并根据收集到的信息进行统计,绘制了尚不完整的统计图.请你根据统计图中所提供的信息解答下列问题:
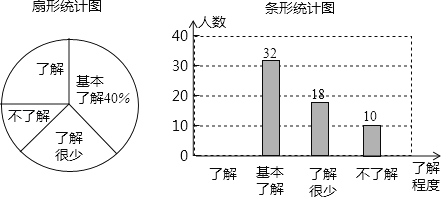
(1)在这次活动中抽查了多少名中学生?
(2)若该中学共有学生1600人,请根据上述调查结果,估计该中学学生中对校园安全知识达到“了解”程度的人数.
(3)若从对校园安全知识达到“了解程度的2个女生和2个男生中随机抽取2人参加校园安全知识竞赛,请用树状图或列表法求出恰好抽到1个男生和1个女生的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在矩形ABCD中,AB=8,AD=6,点E为AB上一点,AE=2![]() ,点F在AD上,将△AEF沿EF折叠,当折叠后点A的对应点A′恰好落在BC的垂直平分线上时,折痕EF的长为_____.
,点F在AD上,将△AEF沿EF折叠,当折叠后点A的对应点A′恰好落在BC的垂直平分线上时,折痕EF的长为_____.
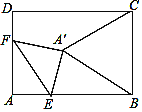
查看答案和解析>>
科目: 来源: 题型:
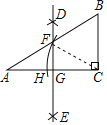
【题目】如图,在△ABC中,∠ACB=90°,分别以点A、C为圆心,以大于![]() AC的长为半径画弧,两弧相交于点D和E,作直线DE交AB于点F,交AC于点G,连接CF,以点C为圆心,以CF的长为半径画弧,交AC于点H.若∠A=30°,BC=2,则AH的长是( )
AC的长为半径画弧,两弧相交于点D和E,作直线DE交AB于点F,交AC于点G,连接CF,以点C为圆心,以CF的长为半径画弧,交AC于点H.若∠A=30°,BC=2,则AH的长是( )
A. ![]() B. 2C.
B. 2C. ![]() +1D. 2
+1D. 2![]() ﹣2
﹣2
查看答案和解析>>
科目: 来源: 题型:
【题目】已知一次函数y1=kx+n(n<0)和反比例函数y2=![]() (m>0,x>0).
(m>0,x>0).
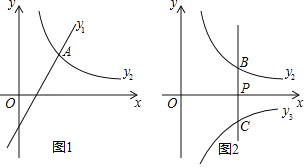
(1)如图1,若n=﹣2,且两个函数的图象都经过点A(3,4).
①求m、k的值;
②直接写出当y1>y2时x的范围: ;
(2)如图2,过点P(1,0)作y轴的平行线l与函数y2的图象相交于点B、与反比例函数y3=![]() (x>0)的图象相交于点C.
(x>0)的图象相交于点C.
①若k=2,直线l与函数,的图象相交点D.当点B、C、D中的一点到另外两点的距离相等时,求m﹣n的值;
②过点B作x轴的平行线与函数y1的图象相交与点E.当m﹣n的值取不大于1的任意实数时,点B、C间的距离与点B、E间的距离之和d始终是一个定值.求此时k的值及定值d.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,△ABC与△CDE为等腰直角三角形,∠BAC=∠DEC=90°,连接AD,取AD中点P,连接BP,并延长到点M,使BP=PM,连接AM、EM、AE,将△CDE绕点C顺时针旋转.
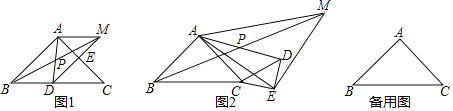
(1)如图①,当点D在BC上,E在AC上时,AE与AM的数量关系是______,∠MAE=______;
(2)将△CDE绕点C顺时针旋转到如图②所示的位置,(1)中的结论是否仍然成立,若成立,请给出证明,若不成立,请说明理由;
(3)若CD=![]() BC,将△CDE由图①位置绕点C顺时针旋转α(0°<α<360°),当ME=
BC,将△CDE由图①位置绕点C顺时针旋转α(0°<α<360°),当ME=![]() CD时,请直接写出α的值.
CD时,请直接写出α的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】图1是某小区入口实景图,图2是该入口抽象成的平面示意图.已知入口BC宽3.9米,门卫室外墙AB上的O点处装有一盏路灯,点O与地面BC的距离为3.3米,灯臂OM长为1.2米(灯罩长度忽略不计),∠AOM=60°.
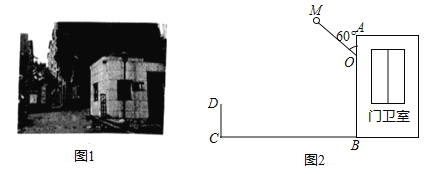
(1)求点M到地面的距离;
(2)某搬家公司一辆总宽2.55米,总高3.5米的货车从该入口进入时,货车需与护栏CD保持0.65米的安全距离,此时,货车能否安全通过?若能,请通过计算说明;若不能,请说明理由.(参考数据:![]() 1.73,结果精确到0.01米)
1.73,结果精确到0.01米)
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知∠MON=90°,A是∠MON内部的一点,过点A作AB⊥ON,垂足为点B,AB=3厘米,OB=4厘米,动点E、F同时从O点出发,点E以1.5厘米/秒的速度沿ON方向运动,点F以2厘米/秒的速度沿OM方向运动,EF与OA交于点C,连接AE,当点E到达点B时,点F随之停止运动,设运动时间为t秒(t>0).
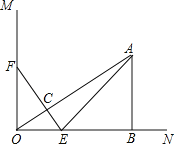
(1)当t=1秒时,△EOF与△ABO是否相似?请说明理由;
(2)在运动过程中,不论t取何值,总有EF⊥OA,为什么?
(3)在运动过程中,是否存在某一时刻t,使得△AEB与△OEF相似?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com