
科目: 来源: 题型:
【题目】在平面直角坐标系中,O为坐标原点,二次函数y=x2+bx+c的图象与x轴交于A,B两点,与y轴的负半轴相交于点C(如图),点C的坐标为(0,﹣3),且BO=CO.
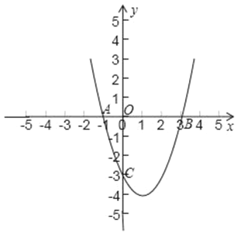
(1)求出B点坐标和这个二次函数的解析式;
(2)求△ABC的面积;
(3)设这个二次函数的图象的顶点为M,求AM的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】某超市以20元/千克的进货价购进了一批绿色食品,如果以30元/千克销售这些绿色食品,那么每天可售出400千克.由销售经验可知,每天的销售量y(千克)与销售单价x(元)(x≥30)存在如图所示的一次函数关系.
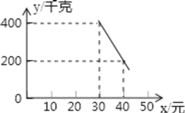
(1)试求出y与x的函数关系式;
(2)设该超市销售该绿色食品每天获得利润w元,当销售单价为何值时,每天可获得最大利润?最大利润是多少?
查看答案和解析>>
科目: 来源: 题型:
【题目】在一场足球比赛中,一球员从球门正前方10米处起脚射门,当球飞行的水平距离为6米时达到最高点,此时球高为3米.
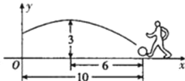
(1)如图建立直角坐标系,当球飞行的路线为一抛物线时,求此抛物线的解析式.
(2)已知球门高为2.44米,问此球能否射中球门(不计其它情况).
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,反比例函数y1=![]() 的图象与一次函数y2=ax+b的图象相交于点A(1,4)和B(﹣2,n).
的图象与一次函数y2=ax+b的图象相交于点A(1,4)和B(﹣2,n).
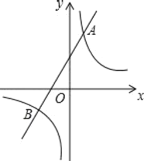
(1)求反比例函数与一次函数的解析式;
(2)请根据图象直接写出y1<y2时,x的取值范围.
查看答案和解析>>
科目: 来源: 题型:
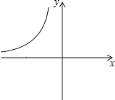
【题目】如图,反比例函数![]() 的图象的一支在平面直角坐标系中的位置如图所示,根据图象回答下列问题:
的图象的一支在平面直角坐标系中的位置如图所示,根据图象回答下列问题:
(1)图象的另一支在第________象限;在每个象限内,![]() 随
随![]() 的增大而________;
的增大而________;
(2)常数![]() 的取值范围是________;
的取值范围是________;
(3)若此反比例函数的图象经过点![]() ,求
,求![]() 的值.点
的值.点![]() 是否在这个函数图象上?点
是否在这个函数图象上?点![]() 呢?
呢?
查看答案和解析>>
科目: 来源: 题型:
【题目】对于反比例函数y=![]() ,下列说法不正确的是( )
,下列说法不正确的是( )
A.图象分布在第一、三象限
B.当x>0时,y随x的增大而减小
C.图象经过点(2,3)
D.若点A(x1,y1),B(x2,y2)都在图象上,且x1<x2,则y1<y2
查看答案和解析>>
科目: 来源: 题型:
【题目】综合与实践探究几何元素之间的关系
问题情境:四边形ABCD中,点O是对角线AC的中点,点E是直线AC上的一个动点(点E与点C,O,A都不重合),过点A,C分别作直线BE的垂线,垂足分别为F,G,连接OF,OG.
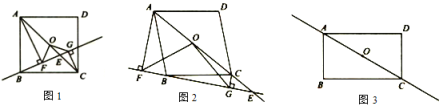
(1)初步探究:
如图1,已知四边形ABCD是正方形,且点E在线段OC上,求证![]() ;
;
(2)深入思考:请从下面A,B两题中任选一题作答,我选择_______题.
A.探究图1中OF与OG的数量关系并说明理由;
B.如图2,已知四边形ABCD为菱形,且点E在AC的延长线上,其余条件不变,探究OF与OG的数量关系并说明理由;
(3)拓展延伸:请从下面AB两题中任选一题作答,我选择_______题.
如图3,已知四边形ABCD为矩形,且![]() ,
,![]() .
.
A.点E在直线AC上运动的过程中,若![]() ,则FG的长为________.
,则FG的长为________.
B.点E在直线AC上运动的过程中,若![]() ,则FG的长为________.
,则FG的长为________.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知菱形ABCD中,![]() ,点E是BC边上的一点(不与B,C重合),以BE为边构造菱形BEFG,使点G落在AB的延长线上,连接BD,GE,射线FE交BD于点H.
,点E是BC边上的一点(不与B,C重合),以BE为边构造菱形BEFG,使点G落在AB的延长线上,连接BD,GE,射线FE交BD于点H.
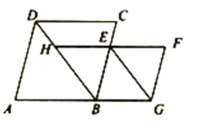
(1)求证:四边形BGEH是平行四边形;
(2)请从下面AB两题中任选一题作答,我选择______题.
A.若四边形BGEH为菱形,则BD的长为_____.
B.连接HC,CF,BF,若![]() ,且四边形BHCF为矩形,则CF的长为______.
,且四边形BHCF为矩形,则CF的长为______.
查看答案和解析>>
科目: 来源: 题型:
【题目】阅读下列材料,完成相应的任务:
我们知道,利用尺规作已知线段的垂直平分线可以得到该线段的中点、四等分点、……怎样得到线段的三等分点呢?如图,已知线段MN,用尺规在MN上求作点P,使![]() .
.
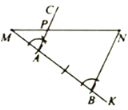
小颖的作法是:
①作射线MK(点K不在直线MN上);
②在射线MK上依次截取线段MA,AB,使![]() ,连接BN;
,连接BN;
③作射线![]() ,交MN于点P点P即为所求作的点.
,交MN于点P点P即为所求作的点.
小颖作法的理由如下:
∵![]() (作法),∴
(作法),∴![]()
∵![]() (已知),
(已知),![]() (等量代换)
(等量代换)
∵![]() (线段和差定义),∴
(线段和差定义),∴![]() (等量代换,等式性质)
(等量代换,等式性质)
数学思考:(1)小颖作法理由中所缺的依据是:________________________________.
拓展应用:(2)如图,已知线段a,b,c,求作线段d,使![]()
a. ![]() b.
b. ![]() c.
c. ![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】为倡导积极健康的生活方式、丰富居民生活,区推出系列文化活动,其中的乒乓球比赛采用单循环赛制(即每两名参赛者之间都要进行一场比赛)经统计,此次乒乓球比赛男子组共要进行28场单打.
(1)参加此次乒乓球男子单打比赛的选手有多少名?
(2)在系列文化活动中,社区与某旅行社合作组织“丰收节”采摘活动收费标准是:如果人数不超过20人,每人收费200元;如果超过20人,每增加1人,每人费用都减少5元经统计,社区共支付“采摘活动”费用4500元求参加此次“丰收节”采摘的人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com