【题目】 如图①，在中，，是过的一条直线，且，在的异侧，于，于．

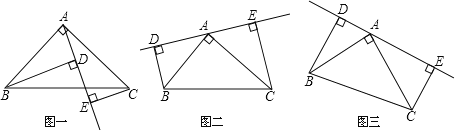
（1）填空：线段与、之间的数量关系为________；

（2）若直线绕点旋转到如图②位置时（），其他条件不变，判断与，之间的数量关系，并说明理由．

（3）若直线绕点旋转到如图③位置时（），其他条件不变，则与，的关系又怎样？请写出结果，不必证明．

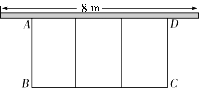
（1）求S关于x的函数关系式及自变量的取值范围；

（2）求所围成花圃的最大面积.

【题目】如图，一圆弧形桥拱的圆心为，拱桥的水面跨度米，桥拱到水面的最大高度为米．求：

桥拱的半径；

现水面上涨后水面跨度为米，求水面上涨的高度为________米．

①b2﹣4ac=0；

②4a+2b+c＜0；

③3a+c=0；

④若（﹣5，y1），（2，y2）是抛物线上的两点，则y1＞y2，

其中正确的是（ ）

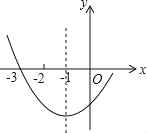
A．1个 B．2个 C．3个 D．4个

A．12寸 B．13寸 C．24寸 D．26寸

【题目】如图，抛物线交轴于、两点，交轴于点，点坐标为，以为直径作，与抛物线交于轴上同一点，连接、.

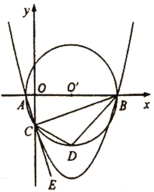
（1）求抛物线的解析式；

（2）点是延长线上一点，的平分线交于点，连接，求直线的解析式；

（3）在（2）的条件下，抛物线上是否存在点，使得？若存在，求出点坐标；若不存在，请说明理由.

【题目】（1）解方程：

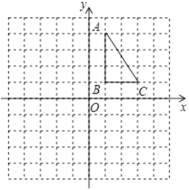
（2）如图，正方形网格中，每个小正方形的边长都是一个单位长度，在平面直角坐标系内，的三个顶点坐标分别为，，.

①画出关于轴对称的；

②画出绕点逆时针旋转后的；

③在②的条件下，求线段扫过的面积（结果保留）.

【题目】小飞研究二次函数（为常数）性质时得出如下结论：

①这个函数图象的顶点始终在直线上；

②存在一个的值，使得函数图象的顶点与轴的两个交点构成等腰直角三角形；

③点与点在函数图象上，若，，则；

④当时，随的增大而增大，则的取值范围为.老师检查以后，发现其中有一个错误的结论，这个错误的结论的序号是：______.

【题目】2019年中国北京世界园艺博览会(以下简称“世园会”)于4月29日至10月7日在北京延庆区举行．世园会为满足大家的游览需求，倾情打造了4条各具特色的趣玩路线，分别是：．“解密世园会”、．“爱我家，爱园艺”、．“园艺小清新之旅”和．“快速车览之旅”．李欣和张帆都计划暑假去世园会，他们各自在这4条线路中任意选择一条线路游览，每条线路被选择的可能性相同．

(1)李欣选择线路．“园艺小清新之旅”的概率是多少？

(2)用画树状图或列表的方法，求李欣和张帆恰好选择同一线路游览的概率．

【题目】 交通工程学理论把在单向道路上行驶的汽车看成连续的流体，并用流量、速度、密度三个概念描述车流的基本特征，其中流量（辆/小时）指单位时间内通过道路指定断面的车辆数；速度（千米/小时）指通过道路指定断面的车辆速度，密度（辆/千米）指通过道路指定断面单位长度内的车辆数.

为配合大数据治堵行动，测得某路段流量与速度之间关系的部分数据如下表：

（1）根据上表信息，下列三个函数关系式中，刻画，关系最准确的是____.（只填上正确答案的序号）

①；②；③.

（2）请利用（1）中选取的函数关系式分析，当该路段的车流速度为多少时，流量达到最大？最大流量是多少？

（3）已知满足.请结合（1）中选取的函数关系式继续解决下列问题.

①市交通运行监控平台显示，当时道路出现轻度拥堵.试分析当车流密度在什么范围时，该路段将出现轻度拥堵；

②在理想状态下，假设前后两车车头之间的距离（米）均相等，求流量最大时的值.