
科目: 来源: 题型:
【题目】如图,在平面直角坐标系中,A (8,0) ,B (0,6),动点M从点A出发沿AO以每秒2个单位长度的速度向原点O运动,同时动点N从点B出发沿折线BO﹣OA向终点A运动,点N在y轴上的速度是每秒3个单位长度,在x轴上的速度是每秒4个单位长度,过点M作x轴的垂线交AB于点C,连结MN、CN.设点M运动的时间为t(秒),△MCN的面积为S(平方单位).
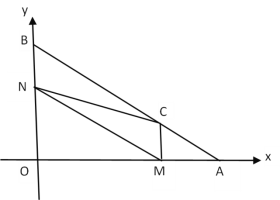
(1)当t为何值时,点M、N相遇?
(2)求△MCN的面积S(平方单位)与时间t(秒)的函数关系式;
(3)当t为何值时,△MCN是等腰三角形?
查看答案和解析>>
科目: 来源: 题型:
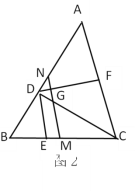
【题目】已知:如图1,在△ABC中,点D在AB上,连接CD. DE平分∠BDC交BC于点E,且DE∥AC, 若F为AC的中点,连接DF.
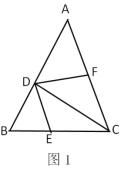
(1)求证:DF⊥DE.
(2)若BE:CE=2:3,S△CDE=9,求△ABC的面积.
(3)如图2,M为BC的中点,过M作MN∥DE交AB于点N,交CD于点G,若BD=a,DG=b.试求CD的长(用a、b的代数式表示).
查看答案和解析>>
科目: 来源: 题型:
【题目】已知:如图所示的一张矩形纸片![]() , 将纸片折叠一次,使点A与C重合,再展开, 折痕EF交AD边于E,交BC边于F,分别连结AF和CE.
, 将纸片折叠一次,使点A与C重合,再展开, 折痕EF交AD边于E,交BC边于F,分别连结AF和CE.
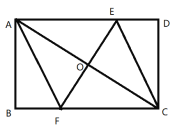
(1)求证:四边形AFCE是菱形;
(2)在线段AC上是否存在一点P,使得![]() ?若存在,请说明点P的位置,并予以证明;若不存在,请说明理由.
?若存在,请说明点P的位置,并予以证明;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,两车分别从路段AB两端同时出发,沿平行路线AC、BD行驶,CE和DF的长分别表示两车到道路AB的距离.
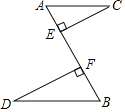
(1)求证:△ACE∽△BDF;
(2)如果两车行驶速度相同,求证:△ACE≌△BDF.
查看答案和解析>>
科目: 来源: 题型:
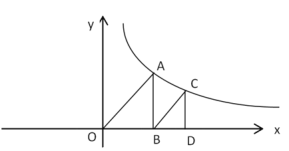
【题目】如下图,反比例函数![]() (
(![]() >0)图象上一点A,连结OA,作AB丄
>0)图象上一点A,连结OA,作AB丄![]() 轴于点B,作BC∥OA交反比例函数图象于点C,作CD丄
轴于点B,作BC∥OA交反比例函数图象于点C,作CD丄![]() 轴于点D,若点A、点C横坐标分别为m、n,则m:n的值为_______________.
轴于点D,若点A、点C横坐标分别为m、n,则m:n的值为_______________.
查看答案和解析>>
科目: 来源: 题型:
【题目】《九章算术》是中国传统数学最重要的著作,奠定了中国传统数学的基本框架.其中第九卷《勾股》章,主要讲述了以测量问题为中心的直角三角形三边互求的关系.其中记载:“今有邑,东西七里,南北九里,各中开门,出东门一十五里有木,问:出南门几何步而见木?”
译文:“今有一座长方形小城,东西向城墙长7里,南北向城墙长9里,各城墙正中均开一城门.走出东门15里处有棵大树,问走出南门多少步恰好能望见这棵树?”(注:1里=300步)
你的计算结果是:出南门几何步而见木( )
A.300步B.315步C.400步D.415步
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,抛物线![]() 与x轴交与A(1,0),B(- 3,0)两点
与x轴交与A(1,0),B(- 3,0)两点
(1)求该抛物线的解析式;
(2)设(1)中的抛物线交y轴与C点,在该抛物线的对称轴上是否存在点Q,使得△QAC的周长最小?若存在,求出Q点的坐标;若不存在,请说明理由.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知△ABC是等腰三角形,顶角∠BAC=![]() (
(![]() <600),D是BC边上的一点,连接AD,线段AD绕点A顺时针旋转
<600),D是BC边上的一点,连接AD,线段AD绕点A顺时针旋转![]() 到AE,过点E作BC的平行线,交AB于点F,连接DE、BE、DF
到AE,过点E作BC的平行线,交AB于点F,连接DE、BE、DF
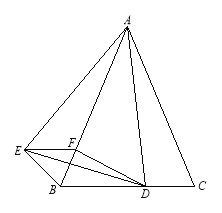
(1)求证:BE=CD
(2)若AD⊥BC,试判断四边形BDFE的形状,并给出证明。
查看答案和解析>>
科目: 来源: 题型:
【题目】中国青少年发展基金会为某地“希望小学”捐赠物资,其中文具和食品共320件,文具比食品多80件.
(1)求文具和食品各多少件;
(2)现计划租用甲、乙两种货车共8辆,一次性将这批文具和食品全部运往该地.已知甲种货车最多可装文具40件和食品10件,乙种货车最多可装文具和食品各20件.则中国青少年发展基金会安排甲、乙两种货车时有几种方案?请你帮助设计出来.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com