
科目: 来源: 题型:
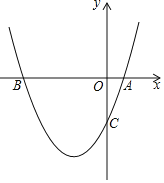
【题目】如图,已知二次函数y=x2+bx+c过点A(1,0),C(0,﹣3)
(1)求此二次函数的解析式及顶点坐标.
(2)设点P是该抛物线上的动点,当△ABP的面积等于△ABC面积的![]() 时,求出点P的坐标.
时,求出点P的坐标.
查看答案和解析>>
科目: 来源: 题型:
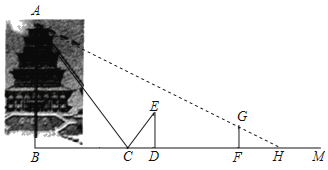
【题目】宝鸡市某学校在“行读石鼓阁”研学活动中,参观了我市中华石鼓园,石鼓阁是宝鸡城市新地标.建筑面积7200平方米,为我国西北第一高阁.小亮想知道石鼓阁的高是多少,他和同学小明对石鼓阁进行测量.测量方案如下:如图,小明在小亮和“石鼓阁”之间的直线BM上平放一平面镜,在镜面上做了一个标记,这个标记在直线BM上的对应位置为点C,镜子不动,小明看着镜面上的标记,他来回走动,走到点D时,看到“石鼓阁”顶端点A在镜面中的像与镜面上的标记重合,这时,测得小明眼睛与地面的高度ED=1.6米,CD=2.2米,然后,在阳光下,小亮从D点沿DM方向走了29.6米,此时“石鼓阁”影子与小亮的影子顶端恰好重合,测得小亮身高1.6米,影长FH=3.2米.已知AB⊥BM,ED⊥BM,GF⊥BM,其中,测量时所使用的平面镜的厚度忽略不计,请你根据题中提供的相关信息,求出“石鼓阁”的高AB的长度.
查看答案和解析>>
科目: 来源: 题型:
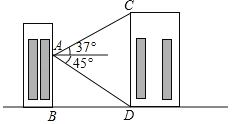
【题目】如图,小明在教学楼A处分别观测对面实验楼CD底部的俯角为45°,顶部的仰角为37°,已知教学楼和实验楼在同一平面上,观测点距地面的垂直高度AB为15m,求实验楼的垂直高度即CD长(精确到1m).
参考值:sin37°=0.60,cos37°=0.80,tan37°=0.75.
查看答案和解析>>
科目: 来源: 题型:
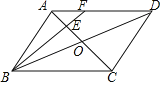
【题目】如图,在ABCD中,AC,BD相交于点O,点E是OA的中点,连接BE并延长交AD于点F,已知S△AEF=4,则下列结论:①![]() =
=![]() ;②△AEF∽△ACD;③S△BCE=36;④S△ABE=12.其中一定正确的是_____(填序号)
;②△AEF∽△ACD;③S△BCE=36;④S△ABE=12.其中一定正确的是_____(填序号)
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,正方形ABCD的对角线上的两个动点M、N,满足AB=![]() MN,点P是BC的中点,连接AN、PM,若AB=6,则当AN+PM取最小值时,线段AN的长度为( )
MN,点P是BC的中点,连接AN、PM,若AB=6,则当AN+PM取最小值时,线段AN的长度为( )
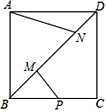
A.4B.2![]() C.6D.3
C.6D.3![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】如图1,在四边形ABCD中,BC∥AD,∠B=90°,AD边落在平面直角坐标系的x轴上,且点A(5,0)、C(0,3)、AD=2.点P从点E(﹣5,0)出发,沿x轴向点A以每秒1个单位长度的速度运动,到达点A时停止运动.运动时间为t秒.
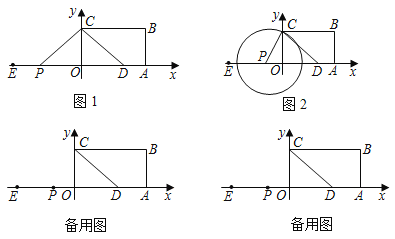
(1)∠BCD的度数为______°.
(2)当t=_____时,△PCD为等腰三角形.
(3)如图2,以点P为圆心,PC为半径作⊙P.
①求当t为何值时,⊙P与四边形ABCD的一边(或边所在的直线)相切.
②当t______时,⊙P与四边形ABCD的交点有两个;当t_____时,⊙P与四边形ABCD的交点有三个.
查看答案和解析>>
科目: 来源: 题型:
【题目】某汽车租贸公司共有汽车50辆,市场调查表明,当租金为每辆每日200元时可全部租出,当租金每提高10元,租出去的车就减少2辆.
(1)当租金提高多少元时,公司的每日收益可达到10120元?
(2)公司领导希望日收益达到10160元,你认为能否实现?若能,求出此时的租金,若不能,请说明理由,
(3)汽车日常维护要定费用,已知外租车辆每日维护费为100元未租出的车辆维护费为50元,当租金为多少元时,公司的利润恰好为5500元?(利润=收益﹣维护费)
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,M,N是以AB为直径的⊙O上的点,且弧AN=弧BN,BM平分∠ABD,MC⊥BD于点C.
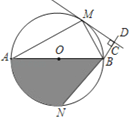
(1)求证:MC是⊙O的切线.
(2)若BC=2,MC=4,求⊙O的直径.
(3)在(2)的条件下,求阴影部分的周长.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,AB为⊙O直径,PA、PC分别与⊙O相切于点A、C,PE⊥PA,PE交OC的延长线于点E.
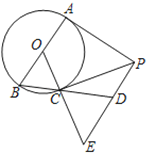
(1)求证:OE=PE;
(2)连接BC并延长交PE于点D,PA=AB,且CE=9,求PE的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,BE是⊙O的直径,半径OA⊥弦BC,垂足为D,连接AE、EC.

(1)若∠AEC=25°,求∠AOB的度数;
(2)若∠A=∠B,EC=4,求⊙O的半径.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com