
科目: 来源: 题型:
【题目】请阅读下列材料:
问题:已知方程![]() ,求一个一元二次方程,使它的根分别是已知方程根的
,求一个一元二次方程,使它的根分别是已知方程根的![]() 倍
倍
解:设所求方程的根为![]() ,则
,则![]() ,所以
,所以![]() .
.
把![]() 代入已知方程,得
代入已知方程,得![]() .
.
化简,得![]()
故所求方程为![]() .
.
这种利用方程的代换求新方程的方法,我们称为“换根法”.
请用阅读材料提供的“换根法”求新方程(要求:把所求方程化为一般形式).
(1)已知方程![]() ,求一个一元二次方程,使它的根分别是已知方程根的相反数,则所求方程为:_______________.
,求一个一元二次方程,使它的根分别是已知方程根的相反数,则所求方程为:_______________.
(2)已知方程![]() ,求一个一元二次方程,使它的根分别是已知方程根的倒数.
,求一个一元二次方程,使它的根分别是已知方程根的倒数.
(3)已知关于![]() 的一元二次方程
的一元二次方程![]() (
(![]() )的两个实数根分别为
)的两个实数根分别为![]() ,
,![]() ,求一元二次方程
,求一元二次方程![]() 的两根.(直接写出结果)
的两根.(直接写出结果)
查看答案和解析>>
科目: 来源: 题型:
【题目】如图所示,在ABCD中,E是CD延长线上的一点,BE与AD交于点F,DE=![]() CD.
CD.
(1)求证:△ABF∽△CEB;
(2)若△DEF的面积为2,求ABCD的面积.

查看答案和解析>>
科目: 来源: 题型:
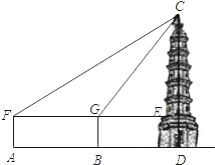
【题目】在一次数学活动课上,老师带领同学们去测量一座古塔CD的高度.他们首先从A处安置测倾器,测得塔顶C的仰角∠CFE=21°,然后往塔的方向前进50米到达B处,此时测得仰角∠CGE=37°,已知测倾器高1.5米,请你根据以上数据计算出古塔CD的高度.
(参考数据:sin37° ![]() ,tan37°
,tan37° ![]() ,sin21°≈
,sin21°≈![]() ,tan21°≈
,tan21°≈![]() )
)
查看答案和解析>>
科目: 来源: 题型:
【题目】已知关于x的方程(x-3)(x-2)-p2=0.
(1)求证:无论p取何值时,方程总有两个不相等的实数根;
(2)设方程两实数根分别为x1、x2,且满足x12+x22=3 x1x2,求实数p的值.
查看答案和解析>>
科目: 来源: 题型:
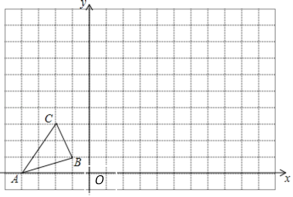
【题目】如图,在 11×16 的网格图中,△ABC 三个顶点坐标分别为 A(﹣4,0),B(﹣1,1),C(﹣2,3).
(1)请画出△ABC 沿x 轴正方向平移4个单位长度所得到的△A1B1C1;
(2)以原点O为位似中心,将(1)中的△A1B1C1 放大为原来的3倍得到△A2B2C2,请在第一象限内画出△A2B2C2,并直接写出△A2B2C2 三个顶点的坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,抛物线y=ax2+6x+c交x轴于A、B两点,交y轴于点C.直线y=x﹣5经过点B、C.
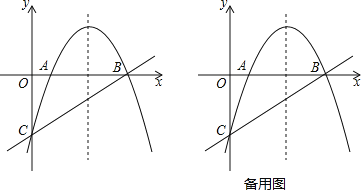
(1)求抛物线的解析式;
(2)过点A作AM⊥BC于点M,过抛物线上一动点P(不与点B、C重合),作直线AM的平行线交直线BC于点Q,若以点A、M、P、Q为顶点的四边形是平行四边形,求点P的横坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,矩形ABCD的一条边AD=8,将矩形ABCD折叠,使得顶点B落在CD边上的P点处,折痕AO与边BC交于点O,连结AP、OP.
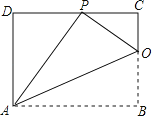
(1)求证:△PDA∽△OCP;
(2)若tan∠PAO=![]() ,求CP的长.
,求CP的长.
查看答案和解析>>
科目: 来源: 题型:
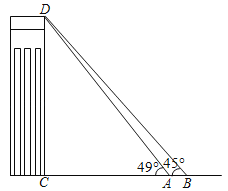
【题目】某校九年级数学兴趣小组在测量某市建筑物CD的高度时,他们在A处测得建筑物顶部D处的仰角为49°,然后他们往CA方向后退了3.4米到达B处(C,A,B在一条直线上),测得建筑物顶部D的仰角恰好为45°,请用他们测量的数据求出建筑物CD的高度.(结果精确到0.1m,参考数据sin49°≈0.75,cos49°≈0.66,tan49°≈1.15).
查看答案和解析>>
科目: 来源: 题型:
【题目】在一个不透明的盒子里装有只有颜色不同的黑、白两种球共40个,小李做摸球试验,她将盒子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回盒子中,不断重复上述过程,下表是试验中的一组统计数据:
摸球的次数n | 100 | 200 | 300 | 500 | 800 | 1000 | 3000 |
摸到白球的次数m | 63 | 124 | 178 | 302 | 488 | 600 | 1800 |
摸到白球的频率 | 0.63 | 0.62 | 0.593 | 0.604 | 0.61 |
|
|
(1)完成上表;
(2)若从盒子中随机摸出一个球,则摸到白球的概率P= ;(结果保留小数点后一位)
(3)估算这个不透明的盒子里白球有多少个?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com