
科目: 来源: 题型:
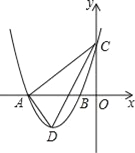
【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx+3与x轴交于A(﹣4,0)、B(﹣l,0)两点,与y轴交于点C,点D是第三象限的抛物线上一动点.
(1)求抛物线的解析式;
(2)设点D的横坐标为m,△ACD的面积为量求出S与m的函数关系式,并确定m为何值时S有最大值,最大值是多少?
(3)若点P是抛物线对称轴上一点,是否存在点P使得∠APC=90°?若存在,请直接写出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】商城某种商品平均每天可销售20件,每件盈利30元,为庆元旦,决定进行促销活动,经调查发现,每件商品每降价1元,商场平均每天可多售出2件.设该商品每件降价![]() 元,请解答下列问题
元,请解答下列问题
(1)用含![]() 的代数式表示:
的代数式表示:
①降价后每售一件盈利 元;
②降价后平均每天售出 件;
(2)在此次促销活动中,商城若要获得最大盈利,每件商品应降价多少元?获得最大盈利多少元?
查看答案和解析>>
科目: 来源: 题型:
【题目】一个不透明的布袋里装有4个大小、质地都相同的乒乓球,球面上分别标有数字1,2,3,4,小明先从布袋中随机摸出一个乒乓球,不放回去,再从剩下的3个球中随机摸出第二个乒乓球.
(1)求小明第一次摸出的乒乓球所标数字是偶数的概率;
(2)请用树状图或列表的方法求两次摸出的乒乓球球面上数字的积为偶数的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知图中的曲线是反比例函数![]() 为常数)图象的一支.
为常数)图象的一支.
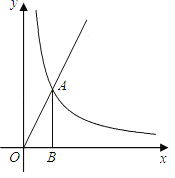
(1)这个反比例函数图象的另一支在第几象限?常数![]() 的取值范围是什么?
的取值范围是什么?
(2)若该函数的图象与正比例函数![]() 的图象在第一象限内的交点为
的图象在第一象限内的交点为![]() ,过
,过![]() 点作
点作![]() 轴的垂线,垂足为
轴的垂线,垂足为![]() ,当
,当![]() 的面积为4时,求点
的面积为4时,求点![]() 的坐标及反比例函数的关系式.
的坐标及反比例函数的关系式.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在每个小正方形边长为![]() 的网格中,
的网格中,![]() 的顶点
的顶点![]() ,
,![]() ,
,![]() 均在格点上,
均在格点上,![]() 为
为![]() 边上的一点.
边上的一点.
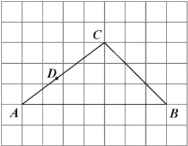
(Ⅰ)线段![]() 的值为______________;
的值为______________;
(Ⅱ)在如图所示的网格中,![]() 是
是![]() 的角平分线,在
的角平分线,在![]() 上求一点
上求一点![]() ,使
,使![]() 的值最小,请用无刻度的直尺,画出
的值最小,请用无刻度的直尺,画出![]() 和点
和点![]() ,并简要说明
,并简要说明![]() 和点
和点![]() 的位置是如何找到的(不要求证明)___________.
的位置是如何找到的(不要求证明)___________.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,某水平地面上建筑物的高度为AB,在点D和点F处分别竖立高是2米的标杆CD和EF,两标杆相隔52米,并且建筑物AB,标杆CD和EF在同一竖直平面内,从标杆CD后退2米到点G处,在G处测得建筑物顶端A和标杆顶端C在同一条直线上;从标杆FE后退4米到点H处,在H处测得建筑物顶端A和标杆顶端E在同一条直线上,求建筑物的高.

查看答案和解析>>
科目: 来源: 题型:
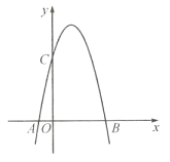
【题目】如图,一个二次函数的图像经过![]() 、
、![]() 、
、![]() 三点,点
三点,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 在
在![]() 轴的正半轴上,且
轴的正半轴上,且![]() .
.
(1)求点![]() 的坐标;
的坐标;
(2)求这个二次函数的解析式;
(3)自变量![]() 在什么范围内时,
在什么范围内时,![]() 随
随![]() 的增大而增大?何时,
的增大而增大?何时,![]() 随
随![]() 的增大而减小
的增大而减小
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系中,已知抛物线![]() 与x轴交于A(-1,0),B(3,0)两点,与y轴交于点C.
与x轴交于A(-1,0),B(3,0)两点,与y轴交于点C.
(1)求该抛物线的解析式;
(2)如图①,若点D是抛物线上一动点,设点D的横坐标为m(0<m<3),连接CD,BD,BC,AC,当△BCD的面积等于△AOC面积的2倍时,求m的值;
(3)若点N为抛物线对称轴上一点,请在图②中探究抛物线上是否存在点M,使得以B,C,M,N为顶点的四边形是平行四边形?若存在,请直接写出所有满足条件的点M的坐标;若不存在,请说明理由.


查看答案和解析>>
科目: 来源: 题型:
【题目】如图,四边形![]() 中,
中,![]() ,将
,将![]() 绕点
绕点![]() 顺时针旋转一定角度后,点
顺时针旋转一定角度后,点![]() 的对应点恰好与点
的对应点恰好与点![]() 重合,得到
重合,得到![]() .
.
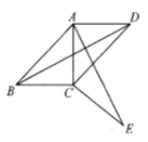
(1)请求出旋转角的度数;
(2)请判断![]() 与
与![]() 的位置关系,并说明理由;
的位置关系,并说明理由;
(3)若![]() ,
,![]() ,试求出四边形
,试求出四边形![]() 的对角线
的对角线![]() 的长.
的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,AB是⊙O的直径,BC为⊙O的切线,D为⊙O上的一点,CD=CB,延长CD交BA的延长线于点E.
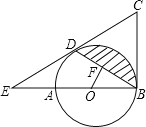
(1)求证:CD为⊙O的切线;
(2)若OF⊥BD于点F,且OF=2,BD=4![]() ,求图中阴影部分的面积.
,求图中阴影部分的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com