
科目: 来源: 题型:
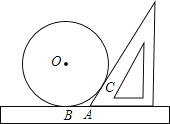
【题目】已知如图:为测量一个圆的半径,采用了下面的方法:将圆平放在一个平面上,用一个含有30°角的三角板和一把无刻度的直尺,按图示的方式测量(此时,⊙O与三角板和直尺分别相切,切点分别为点C、点B),若量得AB=5cm,试求圆的半径以及![]() 的弧长.
的弧长.
查看答案和解析>>
科目: 来源: 题型:
【题目】近年来,我国长江、黄河流域植被遭到破坏,导致土地沙化,洪涝灾害时有发生、沿黄某地区为积极响应和支持“保护母亲河”的倡议,在2000年建立了长100km,宽0.5km的防护林、今年,有关部门为统计这一防护林约有多少棵树,从中选出10块(每块长1km,宽0.5km)统计,数量如下(单位:棵):65110 63200 64600 64700 67300 63300 65100 66600 62800 65500,根据以上数据可知这一防护林约有_____棵树.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,平面直角坐标系内,小正方形网格的边长为1个单位长度,△ABC的顶点A的坐标为(﹣3,4).
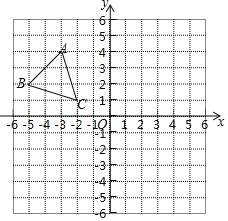
(1)画出△ABC关于y轴的对称图形△A1B1C1,并写出A1的坐标;
(2)画出将△ABC绕原点O逆时针方向旋转90°得到的△A2B2C2,并写出A2的坐标;
(3)求出(2)中点A所经过的路径的长度.
查看答案和解析>>
科目: 来源: 题型:
【题目】临近期末考试,心理专家建议考生可通过以下四种方式进行考前减压:![]() .享受美食,
.享受美食,![]() .交流谈心,
.交流谈心,![]() .体育锻炼,
.体育锻炼,![]() .欣赏艺术.
.欣赏艺术.
(1)随机采访一名九年级考生,选择其中某一种方式,他选择“享受美食”的概率是 .
(2)同时采访两名九年级考生,请用画树状图或列表的方法求他们中至少有一人选择“欣赏艺术”的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】某超市销售一种商品,成本每千克30元,规定每千克售价不低于成本,且不高于70元,经市场调查,每天的销售量y(千克)与每千克售价x(元)满足一次函数关系,部分数据如下表:
售价x(元/千克) | 40 | 50 | 60 |
销售量y(千克) | 100 | 80 | 60 |
(1)求y与x之间的函数表达式;
(2)设商品每天的总利润为W(元),求W与x之间的函数表达式(利润=收入成本);
(3)试说明(2)中总利润W随售价x的变化而变化的情况,并指出售价为多少元时获得最大利润,最大利润是多少?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在Rt△ABC中,∠B=90°,点O在边AB上,以点O为圆心,OA为半径的圆经过点C,过点C作直线MN,使∠BCM=2∠A.
(1)判断直线MN与⊙O的位置关系,并说明理由;
(2)若OA=4,∠BCM=60°,求图中阴影部分的面积.

查看答案和解析>>
科目: 来源: 题型:
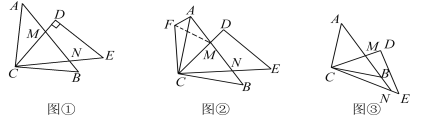
【题目】将两块斜边长相等的等腰直角三角板按如图①摆放,斜边AB分别交CD,CE于M,N点.
(1)如果把图①中的△BCN绕点C逆时针旋转90°得到△ACF,连接FM,如图②,求证:△CMF≌△CMN;
(2)将△CED绕点C旋转,则:
①当点M,N在AB上(不与点A,B重合)时,线段AM,MN,NB之间有一个不变的关系式,请你写出这个关系式,并说明理由;
②当点M在AB上,点N在AB的延长线上(如图③)时,①中的关系式是否仍然成立?
查看答案和解析>>
科目: 来源: 题型:
【题目】定义:由两条与x轴有着相同的交点,并且开口方向相同的抛物线所围成的封闭曲线称为“月牙线”.如图,抛物线C1与抛物线C2组成一个开口向上的“月牙线”,抛物线C1与抛物线C2与x轴有相同的交点M,N(点M在点N的左侧),与y轴的交点分别为A,B且点A的坐标为(0,﹣3),抛物线C2的解析式为y=mx2+4mx﹣12m,(m>0).
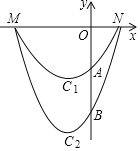
(1)请你根据“月牙线”的定义,设计一个开口向下.“月牙线”,直接写出两条抛物线的解析式;
(2)求M,N两点的坐标;
(3)在第三象限内的抛物线C1上是否存在一点P,使得△PAM的面积最大?若存在,求出△PAM的面积的最大值;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com