
科目: 来源: 题型:
【题目】已知抛物线y=ax2+bx+c(a<0)的对称轴为x=-1,与x轴的一个交点为(2,0).若关于x的一元二次方程ax2+bx+c=p(p>0)有整数根,则p的值有( )
A. 2个B. 3个C. 4个D. 5个
查看答案和解析>>
科目: 来源: 题型:
【题目】已知tan∠MON=2,矩形ABCD的边AB在射线OM上,AD=2,AB=m,CF⊥ON,垂足为点F.
(1)如图(1),作AE⊥ON,垂足为点E. 当m=2时,求线段EF的长度;
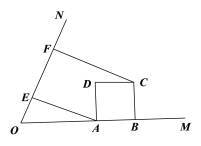
图(1)
(2)如图(2),联结OC,当m=2,且CD平分∠FCO时,求∠COF的正弦值;
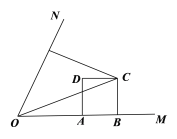
图(2)
(3)如图(3),当△AFD与△CDF相似时,求m的值.
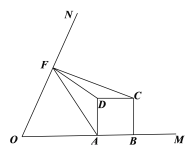
图(3)
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知抛物线y=![]() x2+bx+c过点A(3, 0)、点B(0, 3).点M(m, 0)在线段OA上(与点A、O不重合),过点M作x轴的垂线与线段AB交于点P,与抛物线交于点Q,联结BQ.
x2+bx+c过点A(3, 0)、点B(0, 3).点M(m, 0)在线段OA上(与点A、O不重合),过点M作x轴的垂线与线段AB交于点P,与抛物线交于点Q,联结BQ.
(1)求抛物线表达式;
(2)联结OP,当∠BOP=∠PBQ时,求PQ的长度;
(3)当△PBQ为等腰三角形时,求m的值.

查看答案和解析>>
科目: 来源: 题型:
【题目】以一个等腰直角三角形的腰为边分别向形外做等边三角形,我们把这两个等边三角形重心之间的距离称作这个等腰直角三角形的“肩心距”.如果一个等腰直角三角形的腰长为2,那么它的“肩心距” .
查看答案和解析>>
科目: 来源: 题型:
【题目】下列两个三角形不一定相似的是
A.两条直角边的比都是![]() 的两个直角三角形
的两个直角三角形
B.腰与底的比都是![]() 的两个等腰三角形
的两个等腰三角形
C.有一个内角为![]() 的两个直角三角形
的两个直角三角形
D.有一个内角为![]() 的两个等腰三角形
的两个等腰三角形
查看答案和解析>>
科目: 来源: 题型:
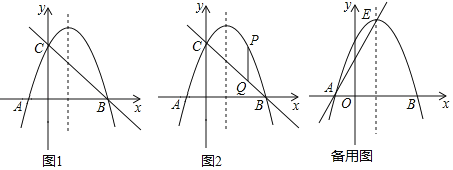
【题目】如图1,抛物线y=﹣x2+2x+3的图象与x轴交于点A、B,与y轴交于点C,连接BC.
(1)求直线BC的解析式;
(2)如图2,点P是抛物线在第一象限内的一点,作PQ∥y轴交BC于Q,当线段PQ的长度最大时,在x轴上找一点M,使PM+CM的值最小,求PM+CM的最小值;
(3)抛物线的顶点为点E,连接AE,在抛物线上是否存在一点N,使得直线AN与直线AE的夹角为45度,若存在请直接写出满足条件的点N的坐标,若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】阅读下列材料:
将一个多位自然数分解为个位与个位之前的数,让个位之前的数减去个位数的两倍,若所得之差能被7整除,则原多位自然数一定能被7整除.也称这个数为“要塞数”.例如:将数1078分解为8和107,107﹣8×2=91,因为91能被7整除,所以1078能被7整除,就称1078为“要塞数”.
完成下列问题:
(1)若一个三位自然数是“要塞数”,且个位数字和百位数字都是7,则这个三位自然数位 ;
(2)若一个四位自然数M是“要塞数”,设M的个位数字为x,十位数字为y,且个位数字与百位数字的和为13,十位数字与千位数字的和也为13,记F(M)=|x﹣y|,求F(M)的最大值.
查看答案和解析>>
科目: 来源: 题型:
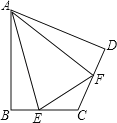
【题目】在四边形ABCD中,AB=AD,∠ABC+∠ADC=180°,E、F分别是边BC,边CD上的两点.
(1)若∠ABC=∠ADC,∠BAE=30°,AD=3,求AE的长;
(2)若∠EAF=![]() ∠BAD,求证:BE+DF=EF.
∠BAD,求证:BE+DF=EF.
查看答案和解析>>
科目: 来源: 题型:
【题目】万州苏宁电器某品牌洗衣机销售情况良好,2018年11月份初该洗衣机每台的进价为2280元,购进了600台该品牌洗衣机.
(1)如果该商场为了减小库存压力,想把购进的600台该品牌洗衣机在11月底全部销售完,商场决定利用打折来促销,每台洗衣机在标价的基础上打8折,这样很快销售一空.要使该商场获得利润不低于72000元,则每台洗衣机的标价应不低于多少元?
(2)该商场决定12月初继续购进600台该品牌洗衣机销售,据悉,2018年12月份因全国经济出现通货膨胀,商品价格进一步上涨,商场决定该品牌洗衣机的销售价格比(1)中的最低标价上涨m%,但实际销售量比11月份下降了![]() m%,如果11月份就按(1)中的最低标价进行销售,且也全部销售完,这样万州苏宁电器12月份的销售额与11月份的销售额持平,求m的值.
m%,如果11月份就按(1)中的最低标价进行销售,且也全部销售完,这样万州苏宁电器12月份的销售额与11月份的销售额持平,求m的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com