
科目: 来源: 题型:
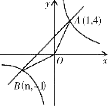
【题目】如图,已知反比例函数![]() 的图象与一次函数y=x+b的图象交于点A(1,4),点B(n,-1).
的图象与一次函数y=x+b的图象交于点A(1,4),点B(n,-1).
(1)求n和b的值;
(2)直接写出一次函数值小于反比例函数值的自变量x的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,四边形OABC是矩形,四边形ADEF是正方形,点A、D在x轴的负半轴上,点C在y轴的正半轴上,点F在AB上,点B、E在反比例函数![]() (k为常数,k ≠0)的图象上,正方形ADEF的面积为16,且BF=2AF,则k值为
(k为常数,k ≠0)的图象上,正方形ADEF的面积为16,且BF=2AF,则k值为
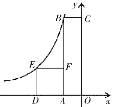
A.-8B.-12C.-24D.-36
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx+c与x轴交于A(﹣2,0),B(8,0)两点,与y轴交于点C,且OC=2OA,抛物线的对称轴x轴交于点D.
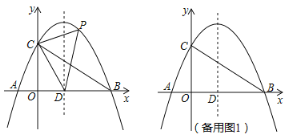
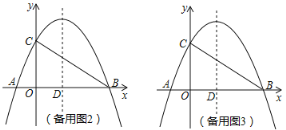
(1)求抛物线的解析式;
(2)点P是第一象限内抛物线上位于对称轴右侧的一个动点,设点P点的横坐标为m,且S△CDP=![]() S△ABC,求m的值;
S△ABC,求m的值;
(3)K是抛物线上一个动点,在平面直角坐标系中是否存在点H,使B、C、K、H为顶点的四边形成为矩形?若存在,直接写出点H的坐标;若不存在,说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】若一个整数的个位数字截去,再从余下的数中,减去个位数的2倍,如果差是7的倍数,则原数能被7整除,如果差太大或心算不易看出是否7的倍数,就需要继续上述[截尾、倍大、相减、验差]的过程,直到能清楚判断为止.
例如,判断126是否7的倍数的过程如下:
12﹣6×2=0,0是7的倍数,所以126是7的倍数;
又例如判断6789是否7的倍数的过程如下:
678﹣9×2=660,66﹣0×2=66,66不是7的倍数,所以6789不是7的倍数.
(1)请判断2019和2555是否能被7整除,并说明理由;
(2)有一个千位数字是1的四位正整数,百位数字与十位数字的和是7,个位数字是十位数字的3倍,且这个四位正整数是7的倍数,求这个四位正整数.
查看答案和解析>>
科目: 来源: 题型:
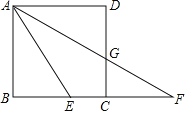
【题目】如图,点E是正方形ABCD的边BC上一点,连接AE,将线段AE绕点E顺时针旋转一定的角度得到EF,点C在EF上,连接AF交边CD于点G.
(1)若AB=4,BF=8,求CE的长;
(2)求证:AE=BE+DG.
查看答案和解析>>
科目: 来源: 题型:
【题目】2018年12月22日下午,第五届全国大众冰雪季暨2018年重庆市首届冰雪运动季系列活动启动仪式在丰都南天湖四季滑雪场园区隆重举行,一系列活动吸引不少中外游客,火锅城人满为患,仅开幕当天,前来丰都某火锅就餐选择红汤火锅和清汤火锅的游客共2500人,其中红汤火锅和清汤火锅的人均消费分别为80元和60元.
(1)开幕当天,若选择红汤火锅的人数不超过清汤火锅人数的1.5倍,求至少有多少人选择清汤火锅?
(2)开幕第二天,前来就餐的人数逐渐减少,与(1)选择清汤火锅的人数最少时相比,选择红汤火锅的人数下降了a%,选择清汤火锅的人数不变,但选择红汤火锅的人均消费增长了a%,选择清汤火锅的人均消费增长了![]() a%,最终开幕第二天两种火锅的销售总额和(1)中选择清汤火锅的人数最少时两种火锅的销售总额相等,求a的值?
a%,最终开幕第二天两种火锅的销售总额和(1)中选择清汤火锅的人数最少时两种火锅的销售总额相等,求a的值?
查看答案和解析>>
科目: 来源: 题型:
【题目】开学初,我县某校开展“新学期、新征程,新气象”入学系列教育活动,训练两天后,为了在合唱中给某班学生恰当地分配声部,该校音乐教师李老师随机抽取学生试唱,根据试唱情况把所抽学生分成A、B、C、D四种声部等级,并根据等级统计结果绘制了如图1和如图2两幅不完整的统计图,请根据图中提供的信息完成以下问题:

(1)扇形统计图中D等对应的圆心角的度数是 °,补全条形统计图;
(2)已知A等声部的同学有一位是男生,李老师准备从这4位同学中随机选择两位同学教其他同学,请用列表法或画树状图的方法求出选中的两名同学恰好是一男一女的概率?
查看答案和解析>>
科目: 来源: 题型:
【题目】丰都县某中学为培养学生综合实践能力,开展了一系列综合实践活动,有一次财商训练活动中,小明同学准备去集市批发两种商品用于活动中交易.预先了解到A、B两种商品的价格之和为27元,小明计划购买B商品的数量比A商品的数量多2件,但一共不超过25件,且每样不少于3件,但小明去购买时发现A商品正打九折销售,而B商品的价格提高了20%,小明决定将A、B产品的购买数量对调,这样实际花费只比计划多8元,已知价格和购买数量均为整数,则小明购买两种商品实际花费为_____元.
查看答案和解析>>
科目: 来源: 题型:
【题目】从﹣3,﹣2,﹣1,0,1,2,3这七个数中,随机抽取一个数记为m,若数m使关于x的分式方程![]() ﹣1=
﹣1=![]() 的解是非负数,且使得二次函数y=(m﹣2)x2+2x+1的图象与x轴有交点,那么满足条件所有m之和是( )
的解是非负数,且使得二次函数y=(m﹣2)x2+2x+1的图象与x轴有交点,那么满足条件所有m之和是( )
A.4B.3C.2D.1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com