
科目: 来源: 题型:
【题目】已知:在平面直角坐标系中,抛物线![]() (
(![]() )交x轴于A、B两点,交y轴于点C,且对称轴为直线x=-2 .
)交x轴于A、B两点,交y轴于点C,且对称轴为直线x=-2 .
(1)求该抛物线的解析式及顶点D的坐标;
(2)若点P(0,t)是y轴上的一个动点,请进行如下探究:
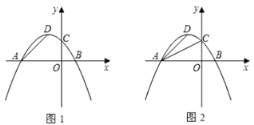
探究一:如图1,设△PAD的面积为S,令W=t·S,当0<t<4时,W是否有最大值?如果有,求出W的最大值和此时t的值;如果没有,说明理由;
探究二:如图2,是否存在以P、A、D为顶点的三角形与Rt△AOC相似?如果存在,求点P的坐标;如果不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,一次函数y=kx+b与反比例函数y=![]() (x>0)的图象交于A(m,6),B(n,3)两点.
(x>0)的图象交于A(m,6),B(n,3)两点.
(1)求一次函数的解析式;
(2)根据图象直接写出kx+b﹣![]() >0时x的取值范围.
>0时x的取值范围.
(3)若M是x轴上一点,且△MOB和△AOB的面积相等,求M点坐标.

查看答案和解析>>
科目: 来源: 题型:
【题目】有一水果店,从批发市场按4元![]() 千克的价格购进10吨苹果,为了保鲜放在冷藏室里,但每天仍有一些苹果变质,平均每天有50千克变质丢弃,且每存放一天需要各种费用300元,据预测,每天每千克价格上涨
千克的价格购进10吨苹果,为了保鲜放在冷藏室里,但每天仍有一些苹果变质,平均每天有50千克变质丢弃,且每存放一天需要各种费用300元,据预测,每天每千克价格上涨![]() 元.
元.
![]() 设x天后每千克苹果的价格为p元,写出p与x的函数关系式;
设x天后每千克苹果的价格为p元,写出p与x的函数关系式;
![]() 若存放x天后将苹果一次性售出,设销售总金额为y元,求出y与x的函数关系式;
若存放x天后将苹果一次性售出,设销售总金额为y元,求出y与x的函数关系式;
![]() 该水果店将这批水果存放多少天后一次性售出,可以获得最大利润,最大利润为多少?
该水果店将这批水果存放多少天后一次性售出,可以获得最大利润,最大利润为多少?
查看答案和解析>>
科目: 来源: 题型:
【题目】为弘扬中华民族传统文化,某市举办了中小学生“国学经典大赛”,比赛项目为:A.唐诗;B.宋词;C.论语;D.三字经.比赛形式分“单人组”和“双人组”.
(1)小华参加“单人组”,他从中随机抽取一个比赛项目,恰好抽中“论语”的概率是多少?
(2)小明和小红组成一个小组参加“双人组”比赛,比赛规则是:同一小组的两名队员的比赛项目不能相同,且每人只能随机抽取一次.则恰好小明抽中“唐诗”且小红抽中“宋词”的概率是多少?小明和小红都没有抽到“三字经”的概率是多少?请用画树状图或列表的方法进行说明.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 是线段
是线段![]() 上的两个动点,且
上的两个动点,且![]() ,过点
,过点![]() ,
,![]() 分别作
分别作![]() ,
,![]() 的垂线相交于点
的垂线相交于点![]() ,垂足分别为
,垂足分别为![]() ,
,![]() .有以下结论:①
.有以下结论:①![]() ;②当点
;②当点![]() 与点
与点![]() 重合时,
重合时,![]() ;③
;③![]() ;④
;④![]() .其中正确的结论有( )
.其中正确的结论有( )

A.1个B.2个C.3个D.4个
查看答案和解析>>
科目: 来源: 题型:
【题目】若抛物线y=x2﹣3x+c与y轴的交点为(0,2),则下列说法正确的是( )
A. 抛物线开口向下
B. 抛物线与x轴的交点为(﹣1,0),(3,0)
C. 当x=1时,y有最大值为0
D. 抛物线的对称轴是直线x=![]()
查看答案和解析>>
科目: 来源: 题型:
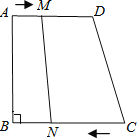
【题目】如图,在梯形ABCD中,AD∥BC,∠B=90°,AB=14cm,AD=15cm,BC=21cm,点M从A点开始,沿AD边向D运动,速度为1厘米/秒,点N从点C开始沿CB边向点B运动,速度为2厘米/秒,设四边形MNCD的面积为S.
(1)写出面积S与时间t之间的函数关系式;
(2)当t为何值时,四边形MNCD是平行四边形?
(3)当t为何值时,四边形MNCD是等腰梯形?
查看答案和解析>>
科目: 来源: 题型:
【题目】已知关于x的一元二次方程![]() .
.
(1)求证:无论k取何实数值,方程总有实数根;
(2)若等腰△ABC的一边长a=6,另两边长b、c恰好是这个方程的两个根,求此三角形的三边长?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系中,点A、B分别在x轴、y轴上,线段OA、OB的长(OA<OB)是一元二次方程x2﹣18x+72=0组的解.点C是直线y=2x与直线AB的交点,点D在线段OC上,OD=2![]() .
.
(1)求点C的坐标;
(2)求直线AD的解析式;
(3)P是直线AD上的点,在平面内是否存在点Q,使以O、A、P、Q为顶点的四边形是菱形?若存在,则求出点Q的坐标;若不存在,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com