
【题目】如图,在平面直角坐标系中,点A、B分别在x轴、y轴上,线段OA、OB的长(OA<OB)是一元二次方程x2﹣18x+72=0组的解.点C是直线y=2x与直线AB的交点,点D在线段OC上,OD=2![]() .
.
(1)求点C的坐标;
(2)求直线AD的解析式;
(3)P是直线AD上的点,在平面内是否存在点Q,使以O、A、P、Q为顶点的四边形是菱形?若存在,则求出点Q的坐标;若不存在,请说明理由.

【答案】(1)C的坐标为(3,6);(2)y=﹣x+6;(3)存在,Q的坐标为(﹣3![]() ,3
,3![]() )或(3
)或(3![]() ,﹣3
,﹣3![]() )或(3,﹣3)或(6,6).
)或(3,﹣3)或(6,6).
【解析】
(1)设直线AB的解析为y=kx+b,解方程x2﹣18x+72=0,得到的解即为OA,OB的长度,进而知道A和B的坐标,再把其横纵坐标分别代入求出k和b的值即可;把求出的解析式和直线y=2x联立解方程组,方程组的解即为点C的坐标.
(2)要求直线AD的解析式,需求出D的坐标,因为点D在直线OC上因此可设D(a,2a),又因为OD=2![]() ,由勾股定理可求出a的值,从而求得点D的坐标,把A、D的坐标代入,利用方程组即可求解.
,由勾股定理可求出a的值,从而求得点D的坐标,把A、D的坐标代入,利用方程组即可求解.
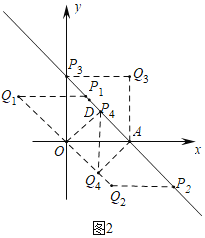
(3)分四种情形:如图2中,当四边形OAP1Q1是菱形时.当四边形OAP2Q2是菱形时.当四边形AOQ3P3是菱形时.当四边形OP4AQ4是菱形时,分别求解即可解决问题.
(1)解方程x2﹣18x+72=0,得到x=6或12,
∵线段OA、OB的长(0A<OB)是方程组的解,
∴OA=6,OB=12,
∴A(6,O),B(0,12),
设直线AB的解析为y=kx+b,
∴![]() ,
,
∴直线AB:y=﹣2x+12,
联立![]() ,
,
解得:![]() ,
,
点C的坐标为(3,6)
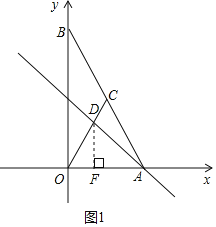
(2)如图1中,设点D:(a,2a),作DF⊥OA于F.
由OD=2![]() ,OF=a,DF=2a,可得a2+(2a)2=(2
,OF=a,DF=2a,可得a2+(2a)2=(2![]() )2,
)2,
得:a=±2,
∵由图得,a>0,
∴a=2.
∴D(2,4),
设直线AD的解析式为y=kx+b
把A(6,0),D(2,4)代入得![]() ,
,
解得![]() ,
,
∴直线AD的解析式为y=﹣x+6;
(3)存在.如图2中,
当四边形OAP1Q1是菱形时,AO=AP1=P1Q1=6,
∵∠DAO=45°,
∴P1(6﹣3![]() ,3
,3![]() ),
),
∴Q1(﹣3![]() ,3
,3![]() ),
),
当四边形OAP2Q2是菱形时,同法可得Q2(3![]() ,﹣3
,﹣3![]() ),
),
当四边形AOQ3P3是菱形时,∵∠AOP3=90°,
∴四边形OAQ3P3是正方形,可得Q3(6,6),
当四边形OP4AQ4是菱形时,
∵∠DAO=∠OAQ4=45°
∴∠P4AQ4=90°,
∴四边形OP4AQ4是正方形,
∴Q4(3,﹣3),
综上所述,满足条件的点Q的坐标为(﹣3![]() ,3
,3![]() )或(3
)或(3![]() ,﹣3
,﹣3![]() )或(3,﹣3)或(6,6).
)或(3,﹣3)或(6,6).


 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() 平分
平分![]() ,交
,交![]() 于点
于点![]() ,点
,点![]() 在
在![]() 上,
上,![]() 经过
经过![]() 两点,交
两点,交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() .
.
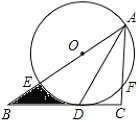
(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)若![]() 的半径是
的半径是![]() ,
,![]() 是弧
是弧![]() 的中点,求阴影部分的面积(结果保留
的中点,求阴影部分的面积(结果保留![]() 和根号).
和根号).
查看答案和解析>>
科目:初中数学 来源: 题型:
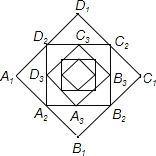
【题目】如图,小宋作出了边长为2的第一个正方形A1B1C1D1,算出了它的面积.然后分别取正方形A1B1C1D1四边的中点A2、B2、C2、D2作出了第二个正方形A2B2C2D2,算出了它的面积.用同样的方法,作出了第三个正方形A3B3C3D3,算出了它的面积…,由此可得,第六个正方形A6B6C6D6的面积是( )
A.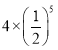 B.
B.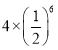 C.
C.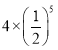 D.
D.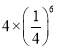
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 是线段
是线段![]() 上的两个动点,且
上的两个动点,且![]() ,过点
,过点![]() ,
,![]() 分别作
分别作![]() ,
,![]() 的垂线相交于点
的垂线相交于点![]() ,垂足分别为
,垂足分别为![]() ,
,![]() .有以下结论:①
.有以下结论:①![]() ;②当点
;②当点![]() 与点
与点![]() 重合时,
重合时,![]() ;③
;③![]() ;④
;④![]() .其中正确的结论有( )
.其中正确的结论有( )

A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学选拔一名青年志愿者:经笔试、面试,结果小明和小丽并列第一.评委会决定通过抓球来确定人选.规则如下:在不透明的布袋里装有除颜色之外均相同的2个红球和1个绿球,小明先取出一个球,记住颜色后放回,然后小丽再取出一个球.若两次取出的球都是红球,则小明胜出;若两次取出的球是一红一绿,则小丽胜出.你认为这个规则对双方公平吗?请用列表法或画树状图的方法进行分析.
查看答案和解析>>
科目:初中数学 来源: 题型:
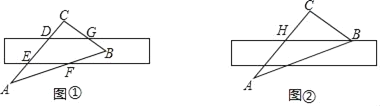
【题目】将直尺摆放在三角板上,使直尺与三角板的边分别交于点D、E、F、G,如图①所示.已知∠CGD=42.
(1)求∠CEF的度数.
(2)将直尺向下平移,使直尺的边缘通过点B,交AC于点H,如图②所示.点H、B的读数分别为4、13.4,求BC的长(精确到0.1)(参考数据:sin42°=0.67,cos42°=0.74,tan42°=0.90)
查看答案和解析>>
科目:初中数学 来源: 题型:
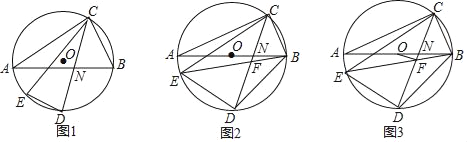
【题目】如图,△ABC内接于⊙O,弦CD平分∠ACB,点E为弧AD上一点,连接CE、DE,CD与AB交于点N.
(1)如图1,求证:∠AND=∠CED;
(2)如图2,AB为⊙O直径,连接BE、BD,BE与CD交于点F,若2∠BDC=90°﹣∠DBE,求证:CD=CE;
(3)如图3,在(2)的条件下,连接OF,若BE=BD+4,BC=![]() ,求线段OF的长.
,求线段OF的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com