
科目: 来源: 题型:
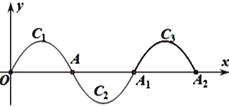
【题目】如图,一段抛物线:y=-x(x-2)(0≤x≤2)记为C1 ,它与x轴交于两点O,A;将C1绕点A旋转180°得到C2 , 交x轴于A1;将C2绕点A1旋转180°得到C3 , 交x轴于点A2 . .....如此进行下去,直至得到C2018 , 若点P(4035,m)在第2018段抛物线上,则m的值为________.
查看答案和解析>>
科目: 来源: 题型:
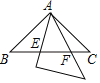
【题目】两个全等的等腰直角三角形,斜边长为2,按如图放置,其中一个三角形45°角的项点与另一个三角形的直角顶点A重合,若三角形ABC固定,当另一个三角形绕点A旋转时,它的角边和斜边所在的直线分别与边BC交于点E、F,设BF=![]() CE=
CE=![]() 则
则![]() 关于
关于![]() 的函数图象大致是( )
的函数图象大致是( )
A. B.
B. C.
C.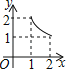 D.
D.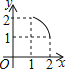
查看答案和解析>>
科目: 来源: 题型:
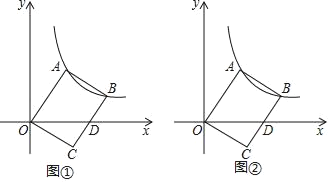
【题目】如图,在平面直角坐标系xOy中,矩形ABCO绕点O旋转,BC边交x轴于点D,反比例函数![]() 经过点A和点B.
经过点A和点B.
(1)如图①,连接AD,若OA=OD=5,且△OAD的面积为10,求反比例函数的解析式;
(2)如图②,连接OB,当∠AOD=60°时,点D恰好是BC的中点,并且△OBD的面积为6![]() ,求OA的长.
,求OA的长.
查看答案和解析>>
科目: 来源: 题型:
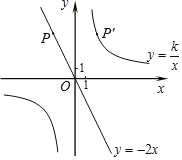
【题目】如图,已知直线y1=﹣2x经过点P(﹣2,a),点P关于y轴的对称点P′在反比例函数y2=![]() (k≠0)的图象上.
(k≠0)的图象上.
(1)求点P的坐标;
(2)求反比例函数的解析式,并直接写出当y2<2时自变量x的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知一次函数![]() 和反比例函数
和反比例函数![]() .
.
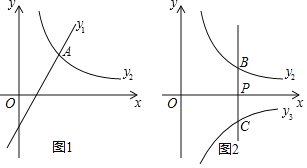
(1)如图1,若![]() ,且函数
,且函数![]() 、
、![]() 的图象都经过点
的图象都经过点![]() .
.
①求![]() ,
,![]() 的值;
的值;
②直接写出当![]() 时
时![]() 的范围;
的范围;
(2)如图2,过点![]() 作
作![]() 轴的平行线
轴的平行线![]() 与函数
与函数![]() 的图象相交于点
的图象相交于点![]() ,与反比例函数
,与反比例函数![]() 的图象相交于点
的图象相交于点![]() .
.
①若![]() ,直线
,直线![]() 与函数
与函数![]() 的图象相交点
的图象相交点![]() .当点
.当点![]() 、
、![]() 、
、![]() 中的一点到另外两点的距离相等时,求
中的一点到另外两点的距离相等时,求![]() 的值;
的值;
②过点![]() 作
作![]() 轴的平行线与函数
轴的平行线与函数![]() 的图象相交于点
的图象相交于点![]() .当
.当![]() 的值取不大于1的任意实数时,点
的值取不大于1的任意实数时,点![]() 、
、![]() 间的距离与点
间的距离与点![]() 、
、![]() 间的距离之和
间的距离之和![]() 始终是一个定值.求此时
始终是一个定值.求此时![]() 的值及定值
的值及定值![]() .
.
查看答案和解析>>
科目: 来源: 题型:
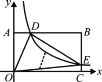
【题目】如图,在以O为原点的直角坐标系中,矩形OABC的两边OC、OA分别在x轴、y轴的正半轴上,反比例函数![]() (x>0)与AB相交于点D,与BC相交于点E,若BD=3AD,且△ODE的面积是9,则k的值是( )
(x>0)与AB相交于点D,与BC相交于点E,若BD=3AD,且△ODE的面积是9,则k的值是( )
A.![]() B.
B.![]() C.
C.![]() D.12
D.12
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,三孔桥横截面的三个孔都呈抛物线形,两个小孔形状、大小都相同,正常水位时,大孔水面常度AB=20米,顶点M距水面6米(即MO=6米),小孔水面宽度BC=6米,顶点N距水面4.5米.航管部门设定警戒水位为正常水位上方2米处借助于图中的平面直角坐标系解答下列问题:
(1)在汛期期间的某天,水位正好达到警戒水位,有一艘顶部高出水面3米,顶部宽4米的巡逻船要路过此处,请问该巡逻船能否安全通过大孔?并说明理由.
(2)在问题(1)中,同时桥对面又有一艘小船准备从小孔迎面通过,小船的船顶高出水面1.5米,顶部宽3米,请问小船能否安全通过小孔?并说明理由.

查看答案和解析>>
科目: 来源: 题型:
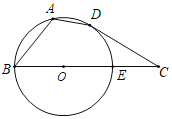
【题目】如图,四边形ABCD的三个顶点A、B、D在⊙O上,BC经过圆心O,且交⊙O于点E,∠A=120°,∠C=30°.
(1)求证:CD是⊙O的切线.
(2)若CD=6,求BC的长.
(3)若⊙O的半径为4,则四边形ABCD的最大面积为 .
查看答案和解析>>
科目: 来源: 题型:
【题目】现有红色和蓝色两个布袋,红色布袋中有三个除标号外完全相同的小球,小球上分别标有数字1,2,3,蓝色布袋中有也三个除标号外完全相同的小球,小球上分别标有数字2,3,4小明先从红布袋中随机取出一个小球,用m表示取出的球上标有的数字,再从蓝布袋中随机取出一个小球,用n表示取出的球上标有的数字.
(1)用列表法或树状图表示出两次取得的小球上所标数字的所有可能结果;
(2)若把m、n分别作为点A的横坐标和纵坐标,求点A(m,n)在函数y=![]() 的图象上的概率.
的图象上的概率.
查看答案和解析>>
科目: 来源: 题型:
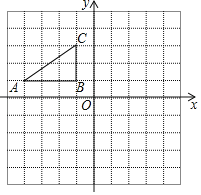
【题目】如图,在平面直角坐标系中,Rt△ABC三个顶点都在格点上,点A、B、C的坐标分别为A(﹣4,1),B(﹣1,1),C(﹣1,3),请解答下列问题:
(1)画出△ABC关于原点O的中心对称图形△A1B1C1;
(2)画出△ABC关于y轴对称图形△A2B2C2,则△A2B2C2与△A1B1C1的位置关系是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com