
科目: 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,AC=4,BC=3.

(1)该三角形的外接圆的半径长等于 ;
(2)用直尺和圆规作出该三角形的内切圆(不写作法,保留作图痕迹),并求出该三角形内切圆的半径长.
查看答案和解析>>
科目: 来源: 题型:
【题目】某中学开展演讲比赛活动,九(1)、九(2)班根据初赛成绩各选出5名选手参加复赛,两个班各选出的5名选手的复赛成绩(满分为100分)如图所示.

(1)根据图填写下表;
平均分 (分) | 中位数 (分) | 众数(分) | 极差 | 方差 | |
九(1)班 | 85 | ______ | 85 | ______ | 70 |
九(2)班 | 85 | 80 | ______ | ______ | ______ |
(2)结合两班复赛成绩的平均数和中位数、极差、方差,分析哪个班级的复赛成绩较好?
(3)如果在每班参加复赛的选手中分别选出2人参加决赛,你认为哪个班的实力更强一些,说明理由.
查看答案和解析>>
科目: 来源: 题型:
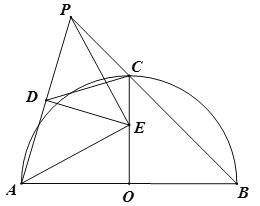
【题目】如图,![]() 为半圆
为半圆![]() 的直径,
的直径,![]() 交
交![]() 于
于![]() ,
,![]() 为
为![]() 延长线上一动点,
延长线上一动点,![]() 为
为![]() 中点,
中点,![]() ,交半径
,交半径![]() 于
于![]() ,连
,连![]() .下列结论:①
.下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() 为定值.其中正确结论的个数为( )
为定值.其中正确结论的个数为( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目: 来源: 题型:
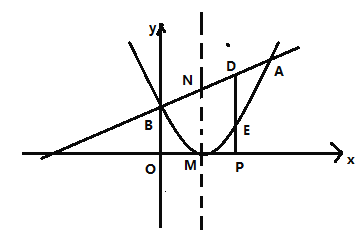
【题目】如图,已知二次函数的图象的顶点坐标为![]() ,直线
,直线![]() 与该二次函数的图象交于
与该二次函数的图象交于![]() ,
,![]() 两点,其中点
两点,其中点![]() 的坐标为
的坐标为![]() ,点
,点![]() 在
在![]() 轴上.
轴上.![]() 是
是![]() 轴上的一个动点,过点
轴上的一个动点,过点![]() 作
作![]() 轴的垂线分别与直线
轴的垂线分别与直线![]() 和二次函数的图象交于
和二次函数的图象交于![]() ,
,![]() 两点.
两点.
(1)求![]() 的值及这个二次函数的解析式;
的值及这个二次函数的解析式;
(2)若点![]() 的横坐标
的横坐标![]() ,求
,求![]() 的面积;
的面积;
(3)当![]() 时,求线段
时,求线段![]() 的最大值;
的最大值;
(4)若直线![]() 与二次函数图象的对称轴交点为
与二次函数图象的对称轴交点为![]() ,问是否存在点
,问是否存在点![]() ,使以
,使以![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形是平行四边形?若存在,请求出此时点
为顶点的四边形是平行四边形?若存在,请求出此时点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】图1是某小区入口实景图,图2是该入口抽象成的平面示意图.已知入口BC宽3.9米,门卫室外墙AB上的O点处装有一盏路灯,点O与地面BC的距离为3.3米,灯臂OM长为1.2米(灯罩长度忽略不计),∠AOM=60°.
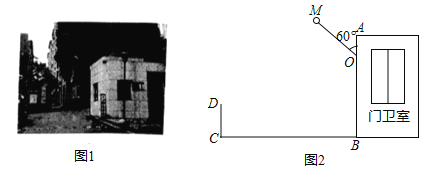
(1)求点M到地面的距离;
(2)某搬家公司一辆总宽2.55米,总高3.5米的货车从该入口进入时,货车需与护栏CD保持0.65米的安全距离,此时,货车能否安全通过?若能,请通过计算说明;若不能,请说明理由.(参考数据:![]() 1.73,结果精确到0.01米)
1.73,结果精确到0.01米)
查看答案和解析>>
科目: 来源: 题型:
【题目】在一个不透明的盒子里装有三个标记为1,2,3的小球(材质、形状、大小等完全相同),甲先从中随机取出一个小球,记下数字为![]() 后放回,同样的乙也从中随机取出一个小球,记下数字为
后放回,同样的乙也从中随机取出一个小球,记下数字为![]() ,这样确定了点
,这样确定了点![]() 的坐标
的坐标![]() .
.
(1)请用列表或画树状图的方法写出点![]() 所有可能的坐标;
所有可能的坐标;
(2)求点![]() 在函数
在函数![]() 的图象上的概率.
的图象上的概率.
查看答案和解析>>
科目: 来源: 题型:
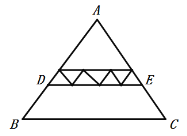
【题目】已知![]() 中,
中,![]() ,
,![]() 的面积为42.
的面积为42.
(1)如图,若点![]() 分别是边
分别是边![]() 的中点,则四边形
的中点,则四边形![]() 的面积是__________.
的面积是__________.

(2)如图,若图中所有的三角形均相似,其中最小的三角形面积为1,则四边形![]() 的面积是___________.
的面积是___________.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,排球运动员站在点O处练习发球,将球从O点正上方2m的A处发出,把球看成点,其运行的高度y(m)与运行的水平距离x(m)满足关系式y=a(x![]() k)2+h.已知球与O点的水平距离为6m时,达到最高2.6m,球网与O点的水平距离为9m.高度为2.43m,球场的边界距O点的水平距离为18m,则下列判断正确的是( )
k)2+h.已知球与O点的水平距离为6m时,达到最高2.6m,球网与O点的水平距离为9m.高度为2.43m,球场的边界距O点的水平距离为18m,则下列判断正确的是( )
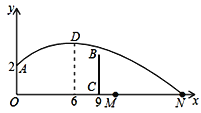
A. 球不会过网 B. 球会过球网但不会出界
C. 球会过球网并会出界 D. 无法确定
查看答案和解析>>
科目: 来源: 题型:
【题目】将一副三角尺(在![]() 中,
中,![]() ,
,![]() ,在
,在![]() 中,
中,![]() ,
,![]() )如图摆放,点
)如图摆放,点![]() 为
为![]() 的中点,
的中点,![]() 交
交![]() 于点
于点![]() ,
,![]() 经过点
经过点![]() ,将
,将![]() 绕点
绕点![]() 顺时针方向旋转
顺时针方向旋转![]() (
(![]() ),
),![]() 交
交![]() 于点
于点![]() ,
,![]() 交
交![]() 于点
于点![]() ,则
,则![]() 的值为( )
的值为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com