
科目: 来源: 题型:
【题目】某商场同时购进甲、乙两种商品共100件,其进价和售价如下表:
商品名称 | 甲 | 乙 |
进价(元/件) | 40 | 90 |
售价(元/件) | 60 | 120 |
设其中甲种商品购进x件,商场售完这100件商品的总利润为y元.
(Ⅰ)写出y关于x的函数关系式;
(Ⅱ)该商场计划最多投入8000元用于购买这两种商品,
①至少要购进多少件甲商品?
②若销售完这些商品,则商场可获得的最大利润是多少元?
查看答案和解析>>
科目: 来源: 题型:
【题目】有四张正面分别标有数字﹣1,0,1,2的不透明卡片,它们除数字外其余全部相同,现将它们背面朝上洗均匀.
(1)随机抽取一张卡片,求抽到数字“﹣1”的概率;
(2)随机抽取一张卡片,然后不放回,再随机抽取一张卡片,请用列表或画树状图的方法求出第一次抽到数字“2”且第二次抽到数字“0”的概率.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,对称轴为直线x=﹣2的抛物线y=x2+bx+c与x轴交于A(﹣5,0),B(1,0)两点,与y轴相交于点C.
(1)求抛物线的解析式,并求出顶点坐标.
(2)若点P在抛物线上,且S△POC=4S△BOC,求出点P的坐标.

查看答案和解析>>
科目: 来源: 题型:
【题目】为了尽快实施“脱贫致富奔小康”宏伟意图,某县扶贫工作队为朝阳沟村购买了一批苹果树苗和梨树苗,已知一棵苹果树苗比一棵梨树苗贵2元,购买苹果树苗的费用和购买梨树苗的费用分别是3500元和2500元.
(1)若两种树苗购买的棵数一样多,求梨树苗的单价;
(2)若两种树苗共购买1100棵,且购买两种树苗的总费用不超过6000元,根据(1)中两种树苗的单价,求梨树苗至少购买多少棵.
查看答案和解析>>
科目: 来源: 题型:
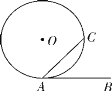
【题目】如图,点A是直线AM与⊙O的交点,点B在⊙O上,BD⊥AM,垂足为D,BD与⊙O交于点C,OC平分∠AOB,∠B=60°.
(1)求证:AM是⊙O的切线;
(2)若⊙O的半径为4,求图中阴影部分的面积(结果保留π和根号).

查看答案和解析>>
科目: 来源: 题型:
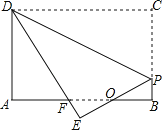
【题目】如图,在矩形ABCD中,E是AB边的中点,沿EC对折矩形ABCD,使B点落在点P处,折痕为EC,连结AP并延长AP交CD于F点,
(1)求证:△CBE≌△CPE;
(2)求证:四边形AECF为平行四边形;
(3)若矩形ABCD的边AB=6,BC=4,求△CPF的面积.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,矩形纸片ABCD,AB=4,BC=3,点P在BC边上,将△CDP沿DP折叠,点C落在点E处,PE、DE分别交AB于点O、F,且OP=OF,则cos∠ADF的值为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,二次函数y=![]() x2+bx+c的图象过点B(0,1)和C(4,3)两点,与x轴交于点D、点E,过点B和点C的直线与x轴交于点A.
x2+bx+c的图象过点B(0,1)和C(4,3)两点,与x轴交于点D、点E,过点B和点C的直线与x轴交于点A.
(1)求二次函数的解析式;
(2)在x轴上有一动点P,随着点P的移动,存在点P使△PBC是直角三角形,请你求出点P的坐标;
(3)若动点P从A点出发,在x轴上沿x轴正方向以每秒2个单位的速度运动,同时动点Q也从A点出发,以每秒a个单位的速度沿射线AC运动,是否存在以A、P、Q为顶点的三角形与△ABD相似?若存在,直接写出a的值;若不存在,说明理由.

查看答案和解析>>
科目: 来源: 题型:
【题目】综合与实践:折纸中的数学
问题背景
在数学活动课上,老师首先将平行四边形纸片ABCD按如图①所示方式折叠,使点C与点A重合,点D落到D′处,折痕为EF.这时同学们很快证得:△AEF是等腰三角形.接下来各学习小组也动手操作起来,请你解决他们提出的问题.
操作发现
(1) “争先”小组将矩形纸片ABCD按上述方式折叠,如图②,发现重叠部分△AEF恰好是等边三角形,求矩形ABCD的长、宽之比是多少?
实践探究
(2)“励志”小组将矩形纸片ABCD沿EF折叠,如图③,使B点落在AD边上的B′处;沿B′G折叠,使D点落在D′处,且B′D′过F点.试探究四边形EFGB′是什么特殊四边形?
(3)再探究:在图③中连接BB′,试判断并证明△BB′G的形状.

查看答案和解析>>
科目: 来源: 题型:
【题目】请阅读下列材料,并完成相应的任务.
人类会作圆并且真正了解圆的性质是在2000多年前,由我国的墨子给出圆的概念:“一中同长也.”.意思说,圆有一个圆心,圆心到圆周的长都相等.这个定义比希腊数学家欧几里得给圆下的定义要早100年.与圆有关的定理有很多,弦切角定理就是其中之一.
我们把顶点在圆上,一边和圆相交,另一边和圆相切的角叫做弦切角.
弦切角定理:弦切角的度数等于它所夹弧所对的圆周角度数.
下面是弦切角定理的部分证明过程:
证明:如图①,AB与⊙O相切于点A.当圆心O在弦AC上时,容易得到∠CAB=90°,所以弦切角∠BAC的度数等于它所夹半圆所对的圆周角度数.
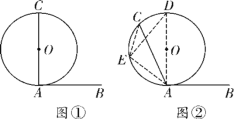
如图②,AB与⊙O相切于点A,当圆心O在∠BAC的内部时,过点A作直径AD交⊙O于点D,在![]() 上任取一点E,连接EC,ED,EA,则∠CED=∠CAD.
上任取一点E,连接EC,ED,EA,则∠CED=∠CAD.
…
任务:
(1)请按照上面的证明思路,写出该证明的剩余部分;
(2)如图③,AB与⊙O相切于点A.当圆心O在∠BAC的外部时,请写出弦切角定理的证明过程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com