
科目: 来源: 题型:
【题目】如图,某小区规划在一个长50米,宽30米的矩形场地ABCD上,修建三条同样宽的道路,使其中两条与AB平行,另一条与AD平行,其余部分种草,若使每块草坪面积都为178平方米,设道路宽度为x米,则( )

A.(50﹣2x)(30﹣x)=178×6
B.30×50﹣2×30x﹣50x=178×6
C.(30﹣2x)(50﹣x)=178
D.(50﹣2x)(30﹣x)=178
查看答案和解析>>
科目: 来源: 题型:
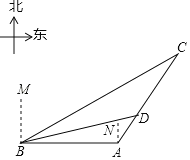
【题目】今年,我国海关总署严厉打击“洋垃圾”违法行动,坚决把“洋垃圾”拒于国门之外.如图,某天我国一艘海监船巡航到A港口正西方的B处时,发现在B的北偏东60°方向,相距150海里处的C点有一可疑船只正沿CA方向行驶,C点在A港口的北偏东30°方向上,海监船向A港口发出指令,执法船立即从A港口沿AC方向驶出,在D处成功拦截可疑船只,此时D点与B点的距离为75![]() 海里.
海里.
(1)求B点到直线CA的距离;
(2)执法船从A到D航行了多少海里?(结果保留根号)
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系中,矩形OABC的对角线OB,AC相交于点D,且BE∥AC,AE∥OB,
(1)求证:四边形AEBD是菱形;
(2)如果OA=3,OC=2,求出经过点E的反比例函数解析式.

查看答案和解析>>
科目: 来源: 题型:
【题目】怡然美食店的A、B两种菜品,每份成本均为14元,售价分别为20元、18元,这两种菜品每天的营业额共为1120元,总利润为280元.
(1)该店每天卖出这两种菜品共多少份?
(2)该店为了增加利润,准备降低A种菜品的售价,同时提高B种菜品的售价,售卖时发现,A种菜品售价每降0.5元可多卖1份;B种菜品售价每提高0.5元就少卖1份,如果这两种菜品每天销售总份数不变,那么这两种菜品一天的总利润最多是多少?
查看答案和解析>>
科目: 来源: 题型:
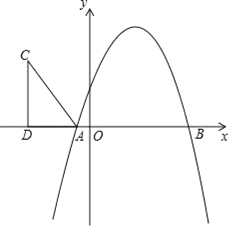
【题目】如图,抛物线y=-x2+bx+c与x轴相交于A(-1,0),B(5,0)两点.
(1)求抛物线的解析式;
(2)在第二象限内取一点C,作CD垂直x轴于点D,链接AC,且AD=5,CD=8,将Rt△ACD沿x轴向右平移m个单位,当点C落在抛物线上时,求m的值;
(3)在(2)的条件下,当点C第一次落在抛物线上记为点E,点P是抛物线对称轴上一点.试探究:在抛物线上是否存在点Q,使以点B、E、P、Q为顶点的四边形是平行四边形?若存在,请出点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】定义:形如y=|G|(G为用自变量表示的代数式)的函数叫做绝对值函数.
例如,函数y=|x﹣1|,y=![]() ,y=|﹣x2+2x+3|都是绝对值函数.
,y=|﹣x2+2x+3|都是绝对值函数.
绝对值函数本质是分段函数,例如,可以将y=|x|写成分段函数的形式:![]() .
.
探索并解决下列问题:
(1)将函数y=|x﹣1|写成分段函数的形式;
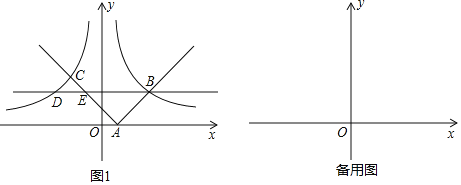
(2)如图1,函数y=|x﹣1|的图象与x轴交于点A(1,0),与函数y=![]() 的图象交于B,C两点,过点B作x轴的平行线分别交函数y=
的图象交于B,C两点,过点B作x轴的平行线分别交函数y=![]() ,y=|x﹣1|的图象于D,E两点.求证△ABE∽△CDE;
,y=|x﹣1|的图象于D,E两点.求证△ABE∽△CDE;
(3)已知函数y=|﹣x2+2x+3|的图象与y轴交于F点,与x轴交于M,N两点(点M在点N的左边),点P在函数y=|﹣x2+2x+3|的图象上(点P与点F不重合),PH⊥x轴,垂足为H.若△PMH与△MOF相似,请直接写出所有符合条件的点P的坐标.
查看答案和解析>>
科目: 来源: 题型:
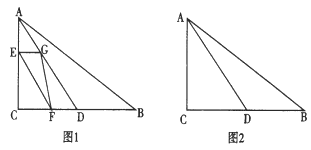
【题目】如图1,△ABC中,∠ACB=90°,AC=4cm,BC=6cm,D是BC的中点.点E从A出发,以acm/s(a>0)的速度沿AC匀速向点C运动;点F同时以1cm/s的速度从点C出发,沿CB匀速向点B运动,其中一个动点到达端点时,另一个动点也随之停止运动,过点E作AC的垂线,交AD于点G,连接EF,FG,设它们运动的时间为t秒(t≥t0).
(1)若t=2,△CEF∽△ABC,求a的值;
(2)当a=![]() 时,以点E、F、D、G为顶点点四边形时平行四边形,求t的值;
时,以点E、F、D、G为顶点点四边形时平行四边形,求t的值;
(3)若a=2,是否存在实数t,使得点△DFG是直角三角形?若存在,请求出t的值;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,四边形ABCD是正方形,点E是平面内异于点A的任意一点,以线段AE为边作正方形AEFG,连接EB,GD.
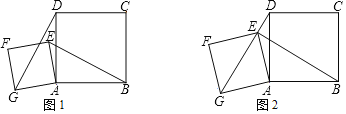
(1)如图1,求证EB=GD;
(2)如图2,若点E在线段DG上,AB=5,AG=3![]() ,求BE的长.
,求BE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com