
科目: 来源: 题型:
【题目】如图,已知抛物线![]() 与
与![]() 轴交于点
轴交于点![]() 、
、![]() ,顶点为M.
,顶点为M.
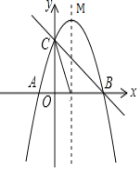
(1)求抛物线的解析式和点M的坐标;
(2)点E是抛物线段BC上的一个动点,设![]() 的面积为S,求出S的最大值,并求出此时点E的坐标;
的面积为S,求出S的最大值,并求出此时点E的坐标;
(3)在抛物线的对称轴上是否存在点P,使得以A、P、C为顶点的三角形是直角三角形?若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图1,![]() 内接于⊙O,过C作射线CP与BA的延长线交于点P,
内接于⊙O,过C作射线CP与BA的延长线交于点P,![]() .
.

(1)求证:CP是⊙O的切线;
(2)若![]() ,
,![]() ,求AB的长;
,求AB的长;
(3)如图2,D是BC的中点,PD与AC交于点E,求证:![]() .
.
查看答案和解析>>
科目: 来源: 题型:
【题目】某高校为了解本校学生出行使用共享单车的情况,随机调查了某天部分出行学生使用共享单车的情况,并整理成如下统计表.
使用次数 | 0 | 1 | 2 | 3 | 4 | 5 |
人数 | 11 | 15 | 23 | 28 | 18 | 5 |
(1)这天部分出行学生使用共享单车次数的中位数是 ,众数是 .
(2)这天部分出行学生平均每人使用共享单车约多少次?(结果保留整数)
(3)若该校某天有1500名学生出行,请你估计这天使用共享单车次数在3次以上(含3次)的学生有多少名.
查看答案和解析>>
科目: 来源: 题型:
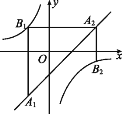
【题目】如图,已知点A1,A2,…,An均在直线![]() 上,点B1,B2,…,Bn均在双曲线
上,点B1,B2,…,Bn均在双曲线![]() 上,并且满足:A1B1⊥x轴,B1A2⊥y轴,A2B2⊥x轴,B2A3⊥y轴,…,AnBn⊥x轴,BnAn+1⊥y轴,…,记点An的横坐标为
上,并且满足:A1B1⊥x轴,B1A2⊥y轴,A2B2⊥x轴,B2A3⊥y轴,…,AnBn⊥x轴,BnAn+1⊥y轴,…,记点An的横坐标为![]() (n为正整数).若
(n为正整数).若![]() ,则
,则![]() __,
__,![]() __.
__.
查看答案和解析>>
科目: 来源: 题型:
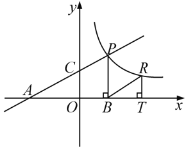
【题目】如图,直线![]() 分别交轴于A、C,点P是该直线与反比例函数在第一象限内的一个交点,PB⊥
分别交轴于A、C,点P是该直线与反比例函数在第一象限内的一个交点,PB⊥![]() 轴于B,且S△ABP=9.
轴于B,且S△ABP=9.
(1)求证:△AOC∽△ABP;
(2)求点P的坐标;
(3)设点R与点P在同一个反比例函数的图象上,且点R在直线PB的右侧,作RT⊥![]() 轴于T,当△BRT与△AOC相似时,求点R的坐标.
轴于T,当△BRT与△AOC相似时,求点R的坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】中学生骑电动车上学的现象越来越受到社会的关注.为此某媒体记者小李随机调查了城区若干名中学生家长对这种现象的态度(态度分为:A:无所谓;B:反对;C:赞成)并将调査结果绘制成图①和图②的统计图(不完整)请根据图中提供的信息,解答下列问题:
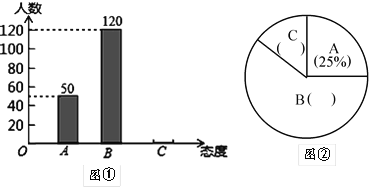
(1)此次抽样调査中.共调査了______名中学生家长;
(2)将图形①、②补充完整;
(3)根据抽样调查结果.请你估计我市城区80000名中学生家长中有多少名家长持反对态度?
查看答案和解析>>
科目: 来源: 题型:
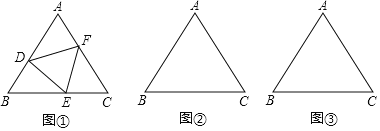
【题目】(概念提出)如图 ①,若正△DEF的三个顶点分别在正△ABC的边AB、BC、AC上,则我们称△DEF是正△ABC的内接正三角形.
(1)求证:△ADF≌△BED.
(问题解决)利用直尺和圆规作正三角形的内接正三角形(保留作图痕迹,不写作法).
(2)如图 ②,正△ABC的边长为a,作正△ABC的内接正△DEF,使△DEF的边长最短,并说明理由;
(3)如图③,作正△ABC的内接正△DEF,使FD⊥AB.
查看答案和解析>>
科目: 来源: 题型:
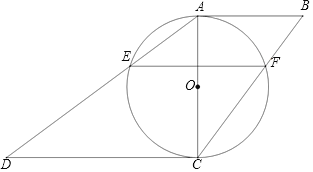
【题目】如图,在四边形ABCD中,AB∥CD,以AC为直径的⊙O交AD于点E,交BC于点F,AB2=BFBC.
(1)求证:AB与⊙O相切;
(2)若![]() .
.
①求证:AC2=ABCD;
②若AC=3,EF=2,则AB+CD= .
查看答案和解析>>
科目: 来源: 题型:
【题目】已知二次函数y=(x﹣m)(x﹣m﹣4)(m为常数).
(1)求证:不论m为何值,该函数的图象与x轴总有两个不同的公共点;
(2)求证:不论m为何值,该函数的图象的顶点纵坐标不变;
(3)若该函数的图象与x轴交点为A、B,与y轴交点为C,当﹣3≤m≤﹣1时,△ABC面积S的取值范围为 .
查看答案和解析>>
科目: 来源: 题型:
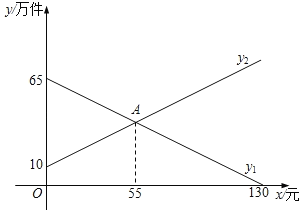
【题目】某商品的市场销售量y1(万件)和生产量y2(万件)都是该商品的定价x(元/件)的一次函数,其函数图象如图所示.
(1)分别求出y1、y2与x之间的函数表达式;
(2)若生产一件该商品成本为10元,未售出的商品一律报废.
①请解释点A的实际意义,并求出此时所获得的利润;
②该商品的定价为多少元时获得的利润最大,最大利润为多少万元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com