
科目: 来源: 题型:
【题目】老师留在小黑板上的题如图所示.小彬说:该抛物线过点![]() ;小明说:
;小明说:![]() ;小颖说:该抛物线在
;小颖说:该抛物线在![]() 轴上截得的线段长为
轴上截得的线段长为![]() .你认为三人的说法中,正确的有( )
.你认为三人的说法中,正确的有( )

A.![]() 个B.
个B.![]() 个C.
个C.![]() 个D.
个D.![]() 个
个
查看答案和解析>>
科目: 来源: 题型:
【题目】某小组做“用频率估计概率”的实验时,绘出的某一结果出现的频率折线图,则符合这一结果的实验可能是( )

A. 抛一枚硬币,出现正面朝上
B. 掷一个正六面体的骰子,出现3点朝上
C. 一副去掉大小王的扑克牌洗匀后,从中任抽一张牌的花色是红桃
D. 从一个装有2个红球1个黑球的袋子中任取一球,取到的是黑球
查看答案和解析>>
科目: 来源: 题型:
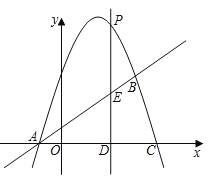
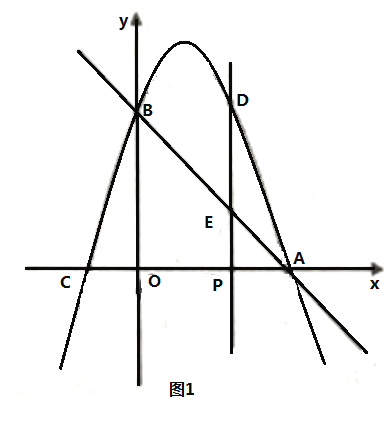
【题目】如图,抛物线y=ax2+bx+c(a≠0)与直线y=x+1相交于A(﹣1,0),B(4,m)两点,且抛物线经过点C(5,0).
(1)求抛物线的解析式.
(2)点P是直线上方的抛物线上的一个动点,求△ABP的面积最大时的P点坐标.
(3)若点P是抛物线上的一个动点(不与点A点B重合),过点P作直线PD⊥x轴于点D,交直线AB于点E.当PE=2ED时,求P点坐标;
(4)设抛物线与y轴交于点F,在抛物线的第一象限内,是否存在一点M,使得AM被FC平分?若存在,请求出点M的坐标;若不存在,说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】某高科技发展公司投资500万元,成功研制出一种市场需求量较大的高科技替代产品,并投入资金1500万元作为固定投资. 已知生产每件产品的成本是40元,在销售过程中发现:当销售单价定为120元时,年销售量为20万件;销售单价每增加10元,年销售量将减少1万件,设销售单价为![]() (元),年销售量为
(元),年销售量为![]() (万件),年获利为
(万件),年获利为![]() (万元)。(年获利=年销售额—生产成本—投资)
(万元)。(年获利=年销售额—生产成本—投资)
(1)试写出![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)请通过计算说明,到第一年年底,当![]() 取最大值时,销售单价
取最大值时,销售单价![]() 定为多少?此时公司是盈利了还是亏损了?
定为多少?此时公司是盈利了还是亏损了?
查看答案和解析>>
科目: 来源: 题型:
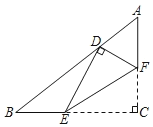
【题目】如图,在Rt△ABC中,∠C=90°,AB=5,BC=4,点E,F分别在边BC,AC上,沿EF所在的直线折叠∠C,使点C的对应点D恰好落在边AB上,若△EFC和△ABC相似,则BD的长为__________.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,矩形OABC的顶点A、C分别在x轴、y轴上,OA=4,OC=3,直线m:y=﹣![]() x从原点O出发,沿x轴正方向以每秒1个单位长度的速度运动,设直线m与矩形OABC的两边分别交于点M,N,直线m运动的时间为t(秒),设△OMN的面积为S,则能反映S与t之间函数关系的大致图象是( )
x从原点O出发,沿x轴正方向以每秒1个单位长度的速度运动,设直线m与矩形OABC的两边分别交于点M,N,直线m运动的时间为t(秒),设△OMN的面积为S,则能反映S与t之间函数关系的大致图象是( )

A. 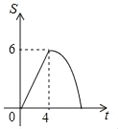 B.
B. 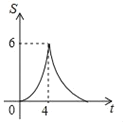 C.
C. 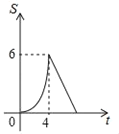 D.
D. 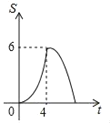
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知一次函数![]() 分别交
分别交![]() 、
、![]() 轴于
轴于![]() 、
、![]() 两点,抛物线
两点,抛物线![]() 经过
经过![]() 、
、![]() 两点,与
两点,与![]() 轴的另一交点为
轴的另一交点为![]() .
.
(1)求![]() 、
、![]() 的值及点
的值及点![]() 的坐标;
的坐标;
(2)动点![]() 从点
从点![]() 出发,以每秒1个单位长度的速度向点
出发,以每秒1个单位长度的速度向点![]() 运动,过
运动,过![]() 作
作![]() 轴的垂线交抛物线于点
轴的垂线交抛物线于点![]() ,交线段
,交线段![]() 于点
于点![]() .设运动时间为
.设运动时间为![]() 秒.
秒.
①当![]() 为何值时,线段
为何值时,线段![]() 长度最大,最大值是多少?(如图1)
长度最大,最大值是多少?(如图1)
②过点![]() 作
作![]() ,垂足为
,垂足为![]() ,连结
,连结![]() ,若
,若![]() 与
与![]() 相似,求
相似,求![]() 的值(如图2)
的值(如图2)

查看答案和解析>>
科目: 来源: 题型:
【题目】如图所示,某学校有一边长为20米的正方形![]() 区域(四周阴影是四个全等的矩形,记为区域甲;中心区是正方形
区域(四周阴影是四个全等的矩形,记为区域甲;中心区是正方形![]() ,记为区域乙).区域甲建设成休闲区,区域乙建成展示区,已知甲、乙两个区域的建设费用如下表:
,记为区域乙).区域甲建设成休闲区,区域乙建成展示区,已知甲、乙两个区域的建设费用如下表:
区域 | 甲 | 乙 |
价格(百元米2) | 6 | 5 |
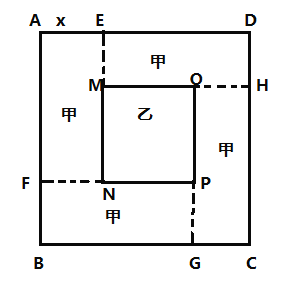
设矩形的较短边![]() 的长为
的长为![]() 米,正方形
米,正方形![]() 区域建设总费用为
区域建设总费用为![]() 百元.
百元.
(1)![]() 的长为 米(用含
的长为 米(用含![]() 的代数式表示);
的代数式表示);
(2)求![]() 关于
关于![]() 的函数解析式;
的函数解析式;
(3)当中心区的边长要求不低于8米且不超过12米时,预备建设资金220000元够用吗?请利用函数的增减性来说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com