
科目: 来源: 题型:
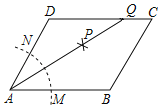
【题目】如图,在平行四边形ABCD中,按以下步骤作图:
①以A为圆心,任意长为半径作弧,分别交AB,AD于点M,N;
②分别以M,N为圆心,以大于![]() MN的长为半径作弧,两弧相交于点P;
MN的长为半径作弧,两弧相交于点P;
③作AP射线,交边CD于点Q.
若QC=1,BC=3,则平行四边形ABCD周长为_____
查看答案和解析>>
科目: 来源: 题型:
【题目】已知,如图,抛物线y=ax2+bx+c(a≠0)的顶点为M(1,9),经过抛物线上的两点A(﹣3,﹣7)和B(3,m)的直线交抛物线的对称轴于点C.
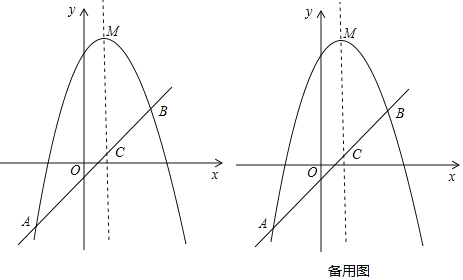
(1)求抛物线的解析式及点B的坐标.
(2)在抛物线上A,M两点之间的部分(不包含A,M两点),是否存在点D,使得S△DAC=2S△DCM?若存在,求出点D的坐标;若不存在,请说明理由.
(3)上下平移直线AB,设平移后的直线与抛物线交与A′,B′两点(A′在左边,B'在右边),且与y轴交与点P(0,n),若∠A′MB′=90°,求n的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】已知,在△ABC和△EFC中,∠ABC=∠EFC=90°,点E在△ABC内,且∠CAE+∠CBE=90°
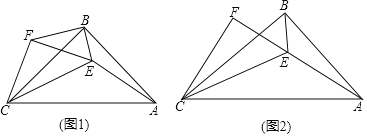
(1)如图1,当△ABC和△EFC均为等腰直角三角形时,连接BF,
①求证:△CAE∽△CBF;
②若BE=2,AE=4,求EF的长;
(2)如图2,当△ABC和△EFC均为一般直角三角形时,若![]() =k,BE=1,AE=3,CE=4,求k的值.
=k,BE=1,AE=3,CE=4,求k的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】为建设天府新区“公园城市”,实现城市生活垃圾减量化、资源化、无害化的目标.近日,成都市天府新区计划在各社区试点实施生活垃圾分类处理活动,取得市民积极响应.某创业公司发现这一商机,研发生产了一种新型家庭垃圾分类桶,并投入市场试营销售.已知该新型垃圾桶成本为每个40元,市场调查发现,该垃圾桶每件售价y(元)与每天的销售量为x(个)的关系如图.为推广新产品及考虑每件利润因素,公司计划每天的销售量不低于1000件且不高于2000件.
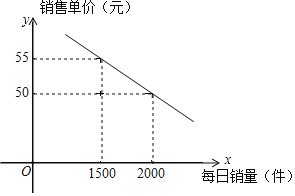
(1)求每件销售单价y(元)与每天的销售量为x(个)的函数关系式;
(2)设该公司日销售利润为W(元),求每天的最大销售利润是多少元?
查看答案和解析>>
科目: 来源: 题型:
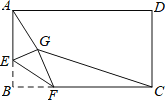
【题目】如图,矩形ABCD中,AB=3,BC=4,点E是A边上一点,且AE=![]() ,点F是边BC上的任意一点,把△BEF沿EF翻折,点B的对应点为G,连接AG,CG,则四边形AGCD的面积的最小值为_____.
,点F是边BC上的任意一点,把△BEF沿EF翻折,点B的对应点为G,连接AG,CG,则四边形AGCD的面积的最小值为_____.
查看答案和解析>>
科目: 来源: 题型:
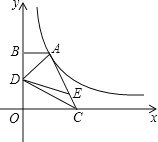
【题目】如图,点A在双曲线y=![]() (k≠0)的第一象限的分支上,AB垂直y轴于点B,点C在x轴正半轴上,OC=2AB,点E在线段AC上,且AE=3EC,点D为OB的中点,连接CD,若△CDE的面积为1,则k的值为_____.
(k≠0)的第一象限的分支上,AB垂直y轴于点B,点C在x轴正半轴上,OC=2AB,点E在线段AC上,且AE=3EC,点D为OB的中点,连接CD,若△CDE的面积为1,则k的值为_____.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线C1:y=ax2+bx﹣1经过点A(﹣2,1)和点B(﹣1,﹣1),抛物线C2:y=2x2+x+1,动直线x=t与抛物线C1交于点N,与抛物线C2交于点M.
(1)求抛物线C1的表达式;
(2)直接用含t的代数式表达线段MN的长;
(3)当△AMN是以MN为直角边的等腰直角三角形时,求t的值.

查看答案和解析>>
科目: 来源: 题型:
【题目】问题情境:如图①,P是⊙O外的一点,直线PO分别交⊙O于点A、B,可以发现PA是点P到⊙O上的点的最短距离.
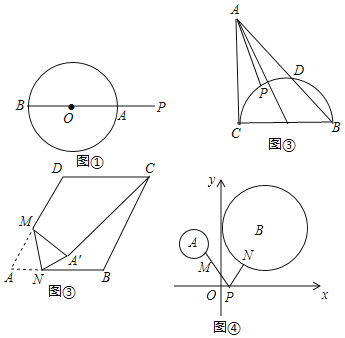
(1)直接运用:如图②,在Rt△ABC中,∠ACB=90°,AC=BC=2,以BC为直径的半圆交AB于D,P是弧CD上的一个动点,连接AP,则AP的最小值是 .
(2)构造运用:如图③,在边长为8的菱形ABCD中,∠A=60°,M是AD边的中点,N是AB边上一动点,将△AMN沿MN所在的直线翻折得到△A′MN,连接A′C,请求出A′C长度的最小值.
(3)综合运用:如图④,平面直角坐标系中,分别以点A(﹣2,3),B(3,4)为圆心,分别以1、2为半径作⊙A、⊙B,M、N分别是⊙A、⊙B上的动点,P为x轴上的动点,则PM+PN的最小值等于 .
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,E点是正方形ABCD的边BC上一点,AB=12,BE=5,△ABE逆时针旋转后能够与△ADF重合.
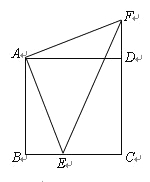
(1)旋转中心是 ,旋转角为 度;
(2)△AEF是 三角形;
(3)求EF的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O分别交AC于点D,交BC于点E,连接ED.
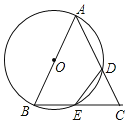
(1)求证:ED=EC;
(2)填空:
①设CD的中点为P,连接EP,则EP与⊙O的位置关系是 ;
②连接OD,当∠B的度数为 时,四边OBED是菱形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com