
科目: 来源: 题型:
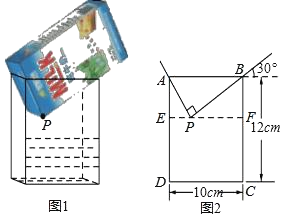
【题目】将一盒足量的牛奶按如图1所示倒入一个水平放置的长方体容器中,当容器中的牛奶刚好接触到点P时停止倒入,图2是它的平面示意图,请根据图中的信息解答下列问题:
(1)填空:AP= cm,PF= cm.
(2)求出容器中牛奶的高度CF.
查看答案和解析>>
科目: 来源: 题型:
【题目】在创客教育理念的指引下,国内很多学校都纷纷建立创客实践室及创客空间,致力于从小培养孩子的创新精神和创造能力,某校开设了“3D”打印、数学编程、智能机器人、陶艺制作“四门创客课程记为A、B、C、D,为了解学生对这四门创客课程的喜爱情况,数学兴趣小组对全校学生进行了随机问卷调查,将调查结果整理后绘制成两幅均不完整的统计图表:
创客课程 | 频数 | 频率 |
“3D”打印 | 36 | 0.45 |
数学编程 | 0.25 | |
智能机器人 | 16 | b |
陶艺制作 | 8 | |
合计 | a | 1 |
请根据图表中提供的信息回答下列问题:
(1)统计表中的a=______,b=______;
(2)“陶艺制作”对应扇形的圆心角为______;
(3)根据调查结果,请你估计该校300名学生中最喜欢“智能机器人”创客课程的人数;
(4)学校为开设这四门课程,预计每生A、B、C、D四科投资比为4:3:6:7,若“3D打印课程每人投资200元,求学校为开设创客课程,需为学生人均投入多少钱?

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系中,边长为2的正方形ABCD在第一象限内,AB∥x轴,点A的坐标为(5,3),己知直线l:y= ![]() x﹣2
x﹣2
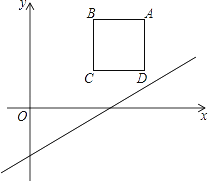
(1)将直线l向上平移m个单位,使平移后的直线恰好经过点A,求m的值
(2)在(1)的条件下,平移后的直线与正方形的边长BC交于点E,求△ABE的面积.
查看答案和解析>>
科目: 来源: 题型:
【题目】为弘扬中华传统文化,某校举办了学生“国学经典大赛”,比赛项目为:A.唐诗;B.宋词;C.元曲;D.论语.比赛形式分“单人组”和“双人组”.
(1)小明参加“单人组”,他从中随机抽取一个比赛项目,则抽到“唐诗”的是 事件,其概率是 ;
(2)若小亮和小丽组成一个小组参加“双人组”比赛,比赛规则是:同一小组的两名队员的比赛项目不能相同,且每人只能随机抽取一次,则小亮和小丽都没有抽到“元曲”的概率是多少?请用画树状图或列表的方法进行说明.
查看答案和解析>>
科目: 来源: 题型:
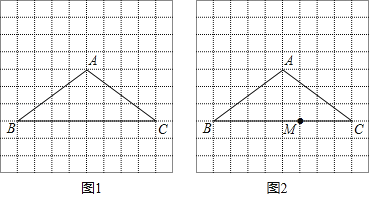
【题目】如图,10×10的网格中,A,B,C均在格点上,诮用无刻度的直尺作直线MN,使得直线MN平分△ABC的周长(留作图痕迹,不写作法)
(1)请在图1中作出符合要求的一条直线MN;
(2)如图2,点M为BC上一点,BM=5.请在AB上作出点N的位置.
查看答案和解析>>
科目: 来源: 题型:
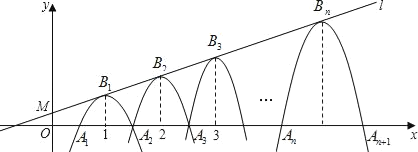
【题目】定义:若抛物线的顶点与x轴的两个交点构成的三角形是直角三角形,则这种抛物线被称为:“直角抛物线”.如图,直线l:y=![]() x+b经过点M(0,
x+b经过点M(0,![]() ),一组抛物线的顶点B1(1,y1),B2(2,y2),B3(3,y3),…Bn(n,yn) (n为正整数),依次是直线l上的点,第一个抛物线与x轴正半轴的交点A1(x1,0)和A2(x2,0),第二个抛物线与x轴交点A2(x2,0)和A3(x3,0),以此类推,若x1=d(0<d<1),当d为_____时,这组抛物线中存在直角抛物线.
),一组抛物线的顶点B1(1,y1),B2(2,y2),B3(3,y3),…Bn(n,yn) (n为正整数),依次是直线l上的点,第一个抛物线与x轴正半轴的交点A1(x1,0)和A2(x2,0),第二个抛物线与x轴交点A2(x2,0)和A3(x3,0),以此类推,若x1=d(0<d<1),当d为_____时,这组抛物线中存在直角抛物线.
查看答案和解析>>
科目: 来源: 题型:
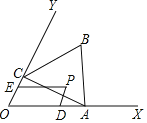
【题目】如图,已知∠XOY=60°,点A在边OX上,OA=2.过点A作AC⊥OY于点C,以AC为一边在∠XOY内作等边三角形ABC,点P是△ABC围成的区域(包括各边)内的一点,过点P作PD∥OY交OX于点D,作PE∥OX交OY于点E.设OD=a,OE=b,则a+2b的取值范围是_____.
查看答案和解析>>
科目: 来源: 题型:
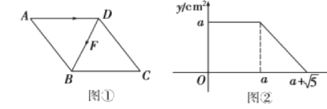
【题目】如图①,点F从菱形ABCD的顶点A出发,沿A→D→B以1cm/s的速度匀速运动到点B.图②是点F运动时,△FBC的面积y(cm![]() )随时间x(s)变化的关系图象,则a的值是__
)随时间x(s)变化的关系图象,则a的值是__
查看答案和解析>>
科目: 来源: 题型:
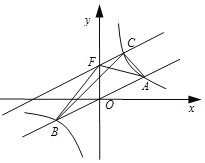
【题目】如图,在平面直角坐标系![]() 中,直线
中,直线![]() 与双曲线
与双曲线![]() 交于
交于![]() 、
、![]() 两点,且点
两点,且点![]() 的坐标为
的坐标为![]() ,将直线
,将直线![]() 向上平移
向上平移![]() 个单位,交双曲线
个单位,交双曲线![]() 于点
于点![]() ,交
,交![]() 轴于点
轴于点![]() ,且
,且![]() 的面积是
的面积是![]() .给出以下结论:(1)
.给出以下结论:(1)![]() ;(2)点
;(2)点![]() 的坐标是
的坐标是![]() ;(3)
;(3)![]() ;(4)
;(4)![]() .其中正确的结论有
.其中正确的结论有![]()
![]()
A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目: 来源: 题型:
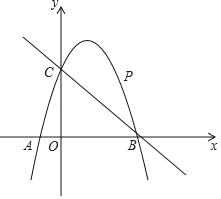
【题目】如图,已知二次函数y=ax2+2x+c的图象经过点C(0,3),与x轴分别交于点A,点B(3,0).点P是直线BC上方的抛物线上一动点.
(1)求二次函数y=ax2+2x+c的表达式;
(2)连接PO,PC,并把△POC沿y轴翻折,得到四边形POP′C.若四边形POP′C为菱形,请求出此时点P的坐标;
(3)当点P运动到什么位置时,四边形ACPB的面积最大?求出此时P点的坐标和四边形ACPB的最大面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com