
科目: 来源: 题型:
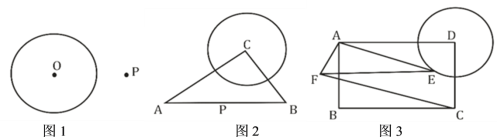
【题目】(1)如图1,![]() 是
是![]() 上一动点,
上一动点,![]() 是
是![]() 外一点,在图中作出
外一点,在图中作出![]() 最小时的点
最小时的点![]() .
.
(2)如图2,![]() 中,
中,![]() ,
,![]() ,
,![]() ,以点
,以点![]() 为圆心的
为圆心的![]() 的半径是
的半径是![]() ,
,![]() 是
是![]() 上一动点,在线段
上一动点,在线段![]() 上确定点
上确定点![]() 的位置,使
的位置,使![]() 的长最小,并求出其最小值.
的长最小,并求出其最小值.
(3)如图3,矩形![]() 中,
中,![]() ,
,![]() ,以
,以![]() 为圆心,
为圆心,![]() 为半径作
为半径作![]() ,
,![]() 为
为![]() 上一动点,连接
上一动点,连接![]() ,以
,以![]() 为直角边作
为直角边作![]() ,
,![]() ,
,![]() ,试探究四边形
,试探究四边形![]() 的面积是否有最大或最小值,如果有,请求出最大或最小值,否则,请说明理由.
的面积是否有最大或最小值,如果有,请求出最大或最小值,否则,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系中,二次函数抛物线![]() 过点
过点![]() 和
和![]() ,对称轴为直线
,对称轴为直线![]() .
.
(1)求二次函数的表达式和顶点![]() 的坐标.
的坐标.
(2)将抛物线在坐标平面内平移,使其过原点,若在平移后,第二象限的抛物线上存在点![]() ,使
,使![]() 为等腰直角三角形,请求出抛物线平移后的表达式,并指出其中一种情况的平移方式.
为等腰直角三角形,请求出抛物线平移后的表达式,并指出其中一种情况的平移方式.
查看答案和解析>>
科目: 来源: 题型:
【题目】小明,小亮都想去观看电影,但是只有一张电影票,他们决定采取抽卡片的办法确定谁去,规定如下:将正面分别标有数字![]() ,
,![]() ,
,![]() 的三张卡片(除数字外其余都同)洗匀后背面朝上放置在桌面上,随机抽出一张记下数字后放回,重新洗匀后背面朝上放置在桌面上,再随机抽出一张记下数字,如果两个数字的积为奇数,则小明去;如果两个数字的积为偶数,则小亮去.
的三张卡片(除数字外其余都同)洗匀后背面朝上放置在桌面上,随机抽出一张记下数字后放回,重新洗匀后背面朝上放置在桌面上,再随机抽出一张记下数字,如果两个数字的积为奇数,则小明去;如果两个数字的积为偶数,则小亮去.
(1)请用列表或树状图的方法表示抽出的两张卡片上的数字积的所有可能出现的结果;
(2)你认为这个规则公平吗?请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】![]() 年我国个人所得税征收办法最新规定:月收入不超过
年我国个人所得税征收办法最新规定:月收入不超过![]() 元的部分不收税;月收入超过
元的部分不收税;月收入超过![]() 元但不超过
元但不超过![]() 元的部分征收
元的部分征收![]() 的所得税;月收入超过
的所得税;月收入超过![]() 元但不超过
元但不超过![]() 元的部分征收
元的部分征收![]() 的所得税
的所得税![]() 国家特别规定月收入指个人工资收入扣除专项附加费后的实际收入(专项附加费就是子女教育费用、住房贷款利息费用、租房的租金、赡养老人、大病医疗费用等费用).如某人月工资收入
国家特别规定月收入指个人工资收入扣除专项附加费后的实际收入(专项附加费就是子女教育费用、住房贷款利息费用、租房的租金、赡养老人、大病医疗费用等费用).如某人月工资收入![]() 元,专项附加费支出
元,专项附加费支出![]() 元,他应缴纳个人所得税为:
元,他应缴纳个人所得税为:![]() (元).
(元).
(1)当月收入超过![]() 元而又不超过
元而又不超过![]() 元时,写出应缴纳个人所得税
元时,写出应缴纳个人所得税![]() (元)与月收入
(元)与月收入![]() (元)之间的关系式;
(元)之间的关系式;
(2)如果某人当月专项附加费支出![]() 元,缴纳个人所得税
元,缴纳个人所得税![]() 元,那么此人本月工资是多少元?
元,那么此人本月工资是多少元?
查看答案和解析>>
科目: 来源: 题型:
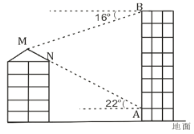
【题目】如图,小明在商城二楼地板![]() 处发现对五层居民楼顶防雨棚一侧斜面
处发现对五层居民楼顶防雨棚一侧斜面![]() 与点
与点![]() 在一条直线上,此时测得
在一条直线上,此时测得![]() ,
,![]() 仰角是
仰角是![]() ,上到九楼在地板边沿
,上到九楼在地板边沿![]() 点测得居民楼顶斜面顶端
点测得居民楼顶斜面顶端![]() 点俯角是
点俯角是![]() ,已知商城每层楼高
,已知商城每层楼高![]() 米,居民楼每层楼高
米,居民楼每层楼高![]() 米,试计算居民楼顶防雨棚一侧斜面
米,试计算居民楼顶防雨棚一侧斜面![]() 的长度.(结果保留精确到
的长度.(结果保留精确到![]() 米)(参考数据:
米)(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
![]() )
)
查看答案和解析>>
科目: 来源: 题型:
【题目】开展阳光体育运动,掌握运动技能,增强身体素质.某校初二年级五月开展了周末一小时兴趣锻炼活动,项目包括:篮球技能、排球技能、足球技能、立定跳远、50米跑,每个同学只选一项参与.王老师为了解学生对各种项目的参与情况,随机调查了部分学生参与哪一类项目(被调查的学生没有不参与的),并将调查结果制成了如下的两个统计图(不完整)请你根据图中所提供的信息,完成下列问题:
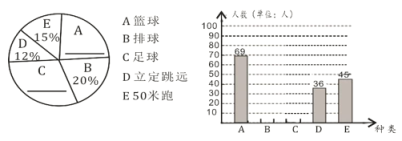
(1)求本次调查的学生人数;
(2)请将两个统计图补充完整,并求出足球项目在扇形统计图中所占圆心角的度数;
(3)若该中学初二年级有![]() 名学生,请估计该校初二学生参与球类项目的人数.
名学生,请估计该校初二学生参与球类项目的人数.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,抛物线![]() 与
与![]() 轴相交于
轴相交于![]() 两点(点
两点(点![]() 位于点
位于点![]() 的左侧),与
的左侧),与![]() 轴相交于点
轴相交于点![]() ,
,![]() 是抛物线的顶点,直线
是抛物线的顶点,直线![]() 是抛物线的对称轴,且点
是抛物线的对称轴,且点![]() 的坐标为
的坐标为![]() .
.
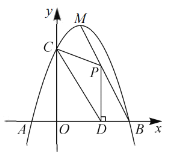
(1)求抛物线的解析式.
(2)已知![]() 为线段
为线段![]() 上一个动点,过点
上一个动点,过点![]() 作
作![]() 轴于点
轴于点![]() .若
.若![]() 的面积为
的面积为![]() .
.
①求![]() 与
与![]() 之间的函数关系式,并写出自变量
之间的函数关系式,并写出自变量![]() 的取值范围;
的取值范围;
②当![]() 取得最值时,求点
取得最值时,求点![]() 的坐标.
的坐标.
(3)在(2)的条件下,在线段![]() 上是否存在点
上是否存在点![]() ,使
,使![]() 为等腰三角形?如果存在,请求出点
为等腰三角形?如果存在,请求出点![]() 的坐标;如果不存在,请说明理由.
的坐标;如果不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】在![]() 中,
中,![]() ,
,![]() 是平面内不与点
是平面内不与点![]() 重合的任意一点,连接
重合的任意一点,连接![]() ,将线段
,将线段![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 得到线段
得到线段![]() ,连接
,连接![]() 是
是![]() 的中点,
的中点,![]() 是
是![]() 的中点.
的中点.
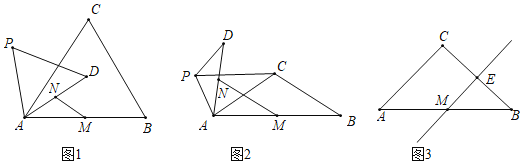
(1)问题发现:
如图1,当![]() 时,
时,![]() 的值是_________,直线
的值是_________,直线![]() 与直线
与直线![]() 相交所成的较小角的度数是________.
相交所成的较小角的度数是________.
(2)类比探究:
如图2,当![]() 时,请写出
时,请写出![]() 的值及直线
的值及直线![]() 与直线
与直线![]() 相交所成的较小角的度数,并说明理由.
相交所成的较小角的度数,并说明理由.
(3)解决问题:
如图3,当![]() 时,若
时,若![]() 是
是![]() 的中点,点
的中点,点![]() 在直线
在直线![]() 上,且点
上,且点![]() 在同一条直线上,请直接写出
在同一条直线上,请直接写出![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com