
科目: 来源: 题型:
【题目】小李在学习了定理“直角三角形斜边上的中线等于斜边的一半”之后做了如下思考,请你帮他完成如下问题:
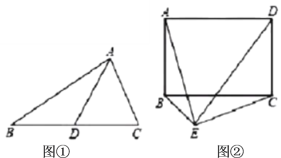
(1)他认为该定理有逆定理:“如果一个三角形某条边上的中线等于该边长的一半,那么这个三角形是直角三角形”应该成立.即如图①,在![]() 中,
中,![]() 是
是![]() 边上的中线,若
边上的中线,若![]() ,求证:
,求证:![]() .
.
(2)如图②,已知矩形![]() ,如果在矩形外存在一点
,如果在矩形外存在一点![]() ,使得
,使得![]() ,求证:
,求证:![]() .(可以直接用第(1)问的结论)
.(可以直接用第(1)问的结论)
(3)在第(2)问的条件下,如果![]() 恰好是等边三角形,请求出此时矩形的两条邻边
恰好是等边三角形,请求出此时矩形的两条邻边![]() 与
与![]() 的数量关系.
的数量关系.
查看答案和解析>>
科目: 来源: 题型:
【题目】抛物线y=x2+bx+c经过点A、B、C,已知A(﹣1,0),C(0,﹣3).
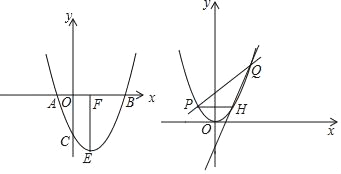
(1)求抛物线的解析式;
(2)如图1,抛物线顶点为E,EF⊥x轴于F点,M(m,0)是x轴上一动点,N是线段EF上一点,若∠MNC=90°,请指出实数m的变化范围,并说明理由.
(3)如图2,将抛物线平移,使其顶点E与原点O重合,直线y=kx+2(k>0)与抛物线相交于点P、Q(点P在左边),过点P作x轴平行线交抛物线于点H,当k发生改变时,请说明直线QH过定点,并求定点坐标.
查看答案和解析>>
科目: 来源: 题型:
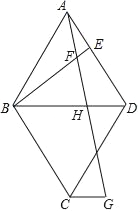
【题目】如图,菱形ABCD中,∠BAD=60°,点E在边AD上,连接BE,在BE上取点F,连接AF并延长交BD于H,且∠AFE=60°,过C作CG∥BD,直线CG、AF交于G.
(1)求证:∠FAE=∠EBA;
(2)求证:AH=BE;
(3)若AE=3,BH=5,求线段FG的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在某一路段,规定汽车限速行驶,交通警察在此限速路段的道路上设置了监测区,其中点C、D为监测点,已知点C、D、B在同一直线上,且AC⊥BC,CD=400米,tan∠ADC=2,∠ABC=35°
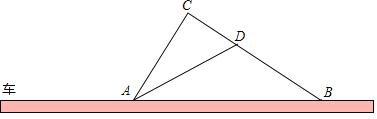
(1)求道路AB段的长(结果精确到1米)
(2)如果道路AB的限速为60千米/时,一辆汽车通过AB段的时间为90秒,请你判断该车是否是超速,并说明理由;参考数据:sin35°≈0.5736,cos35°≈0.8192,tan35°≈0.7002
查看答案和解析>>
科目: 来源: 题型:
【题目】(Ⅰ)如图1,在菱形![]() 中,已知
中,已知![]() ,
,![]() ,抛物线
,抛物线![]() (
(![]() )经过
)经过![]() ,
,![]() ,
,![]() 三点.
三点.
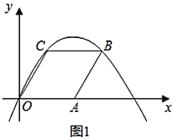
(1)点![]() 的坐标为__________,点
的坐标为__________,点![]() 的坐标为__________;
的坐标为__________;
(2)求抛物线的解析式.
(Ⅱ)如图2,点![]() 是
是![]() 的中点,点
的中点,点![]() 是
是![]() 的中点,直线
的中点,直线![]() 垂直
垂直![]() 于点
于点![]() ,点
,点![]() 在直线
在直线![]() 上.
上.
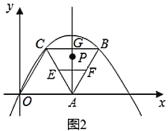
(3)当![]() 的值最小时,则点
的值最小时,则点![]() 的坐标为____________;
的坐标为____________;
(4)在(3)的条件下,连接![]() 、
、![]() 、
、![]() 得
得![]() ,问在抛物线上是否存在点
,问在抛物线上是否存在点![]() ,使得以
,使得以![]() ,
,![]() ,
,![]() 为顶点的三角形与
为顶点的三角形与![]() 相似?若存在,请求出点
相似?若存在,请求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,点![]() 是线段
是线段![]() 上一点,
上一点,![]() ,以点
,以点![]() 为圆心,
为圆心,![]() 的长为半径作⊙
的长为半径作⊙![]() ,过点
,过点![]() 作
作![]() 的垂线交⊙
的垂线交⊙![]() 于
于![]() ,
,![]() 两点,点
两点,点![]() 在线段
在线段![]() 的延长线上,连接
的延长线上,连接![]() 交⊙
交⊙![]() 于点
于点![]() ,以
,以![]() ,
,![]() 为边作
为边作![]() .
.

(1)求证:![]() 是⊙
是⊙![]() 的切线;
的切线;
(2)若![]() ,求四边形
,求四边形![]() 与⊙
与⊙![]() 重叠部分的面积;
重叠部分的面积;
(3)若![]() ,
,![]() ,连接
,连接![]() ,求
,求![]() 和
和![]() 的长.
的长.
查看答案和解析>>
科目: 来源: 题型:
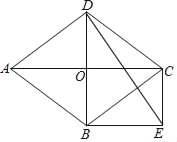
【题目】如图,在菱形ABCD中,对角线AC和BD交于点O,分别过点B、C作BE∥AC,CE∥BD,BE与CE交于点E.
(1)求证:四边形OBEC是矩形;
(2)当∠ABD=60°,AD=2![]() 时,求∠EDB的正切值.
时,求∠EDB的正切值.
查看答案和解析>>
科目: 来源: 题型:
【题目】为了节能减排,我市某校准备购买某种品牌的节能灯,已知3只A型节能灯和5只B型节能灯共需50元,2只A型节能灯和3只B型节能灯共需31元.
(1)求1只A型节能灯和1只B型节能灯的售价各是多少元?
(2)学校准备购买这两种型号的节能灯共200只,要求A型节能灯的数量不超过B型节能灯的数量的3倍,请设计出最省钱的购买方案,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com