
科目: 来源: 题型:
【题目】在平面直角坐标系xOy中,定义点P(x,y)的变换点为P′(x+y,x﹣y).
(1)如图1,如果⊙O的半径为![]() ,
,
①请你判断M(2,0),N(﹣2,﹣1)两个点的变换点与⊙O的位置关系;
②若点P在直线y=x+2上,点P的变换点P′在⊙O的内,求点P横坐标的取值范围.
(2)如图2,如果⊙O的半径为1,且P的变换点P′在直线y=﹣2x+6上,求点P与⊙O上任意一点距离的最小值.

查看答案和解析>>
科目: 来源: 题型:
【题目】如图1,在正方形![]() 中,
中,![]() 是对角线
是对角线![]() 上的一点,点
上的一点,点![]() 在
在![]() 的延长线上,
的延长线上,![]() 交
交![]() 于
于![]() ,
,![]() .
.
(1)求证:![]() ;
;
(2)连接![]() ,若
,若![]() ,求
,求![]() ;
;
(3)如图2,若把正方形![]() 改为菱形
改为菱形![]() ,其他条件不变,当
,其他条件不变,当![]() 时,猜想
时,猜想![]() 与
与![]() 的数量关系,并证明你的猜想.
的数量关系,并证明你的猜想.
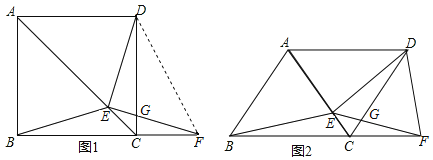
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线y=mx2﹣6mx+9m+1(m≠0).
(1)求抛物线的顶点坐标;
(2)若抛物线与x轴的两个交点分别为A和B点(点A在点B的左侧),且AB=4,求m的值.
(3)已知四个点C(2,2)、D(2,0)、E(5,﹣2)、F(5,6),若抛物线与线段CD和线段EF都没有公共点,请直接写出m的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】吴京同学根据学习函数的经验,对一个新函数y=![]() 的图象和性质进行了如下探究,请帮他把探究过程补充完整
的图象和性质进行了如下探究,请帮他把探究过程补充完整
(1)该函数的自变量x的取值范围是 .
(2)列表:
x | … | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | … |
y | … |
| m | ﹣1 |
| ﹣5 | n | ﹣1 |
|
| … |
表中m= ,n= .
(3)描点、连线
在下面的格点图中,建立适当的平面直角坐标系xOy中,描出上表中各对对应值为坐标的点(其中x为横坐标,y为纵坐标),并根据描出的点画出该数的图象:
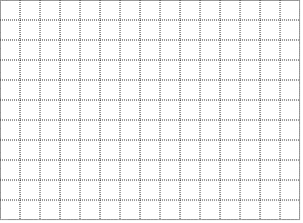
(4)观察所画出的函数图象,写出该函数的两条性质:
① ;
② .
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,函数![]() 的图象与直线y=2x+1交于点A(1,m).
的图象与直线y=2x+1交于点A(1,m).
(1)求k、m的值;
(2)已知点P(n,0)(n≥1),过点P作平行于y轴的直线,交直线y=2x+1于点B,交函数![]() 的图象于点C.横、纵坐标都是整数的点叫做整点.
的图象于点C.横、纵坐标都是整数的点叫做整点.
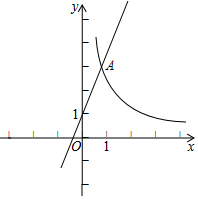
①当n=3时,求线段AB上的整点个数;
②若![]() 的图象在点A、C之间的部分与线段AB、BC所围成的区域内(包括边界)恰有5个整点,直接写出n的取值范围.
的图象在点A、C之间的部分与线段AB、BC所围成的区域内(包括边界)恰有5个整点,直接写出n的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在四边形ABCD中,AD∥BC,BA=BC,BD平分∠ABC.
(1)求证:四边形ABCD是菱形;
(2)过点D作DE⊥BD,交BC的延长线于点E,若BC=5,BD=8,求四边形ABED的周长.
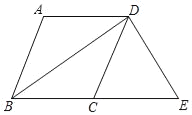
查看答案和解析>>
科目: 来源: 题型:
【题目】事件发生的可能性有大有小,请你把下列事件发生可能性的大小按由小到大的顺序排列起来__________.(只排序号)
①书包里有12本不同科目的教科书,随手摸出一本,恰好是数学书;
②花2元买了一张彩票,就中了500万大奖;
③我抛了两次硬币,都正面向上;
④若![]() ,则
,则![]() 和
和![]() 互为相反数.
互为相反数.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图显示了用计算机模拟随机抛掷一枚硬币的某次实验的结果

下面有三个推断:
①当抛掷次数是100时,计算机记录“正面向上”的次数是47,所以“正面向上”的概率是0.47;
②随着试验次数的增加,“正面向上”的频率总在0.5附近摆动,显示出一定的稳定性,可以估计“正面向上”的概率是0.5;
③若再次用计算机模拟此实验,则当抛掷次数为150时,“正面向上”的频率一定是0.45.
其中合理的是( )
A.①B.②C.①②D.①③
查看答案和解析>>
科目: 来源: 题型:
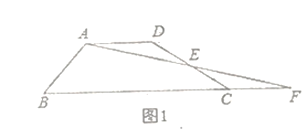
【题目】小明在一次数学兴趣小组活动中,对一个数学问题作如下探究:
问题情境:(1)如图1,四边形![]() 中,
中,![]() ,点
,点![]() 为
为![]() 边的中点,连接
边的中点,连接![]() 并延长交
并延长交![]() 的延长线于点
的延长线于点![]() ,求证:
,求证:![]() ;(
;(![]() 表示面积)
表示面积)
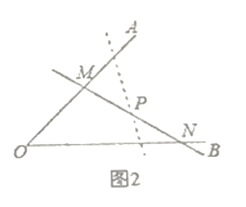
问题迁移:(2)如图2:在已知锐角![]() 内有一个定点
内有一个定点![]() .过点
.过点![]() 任意作一条直线
任意作一条直线![]() 分别交射线
分别交射线![]() 于点
于点![]() .小明将直线
.小明将直线![]() 绕着点
绕着点![]() 旋转的过程中发现,
旋转的过程中发现,![]() 的面积存在最小值,请问当直线
的面积存在最小值,请问当直线![]() 在什么位置时,
在什么位置时,![]() 的面积最小,并说明理由.
的面积最小,并说明理由.
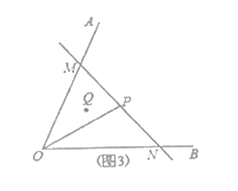
实际应用:(3)如图3,若在道路![]() 之间有一村庄
之间有一村庄![]() 发生疫情,防疫部门计划以公路
发生疫情,防疫部门计划以公路![]() 和经过防疫站
和经过防疫站![]() 的一条直线
的一条直线![]() 为隔离线,建立个面积最小的三角形隔离区
为隔离线,建立个面积最小的三角形隔离区![]() ,若测得
,若测得![]() 试求
试求![]() 的面积.(结果保留根号)(参考数据:
的面积.(结果保留根号)(参考数据:![]() )
)
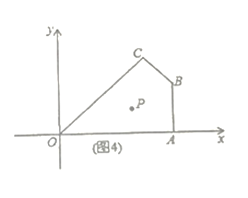
拓展延伸:(4)如图4,在平面直角坐标系中,![]() 为坐标原点,点
为坐标原点,点![]() 的坐标分别为
的坐标分别为![]() ,过点
,过点![]() 的直线
的直线![]() 与四边形
与四边形![]() 一组对边相交,将四边形
一组对边相交,将四边形![]() 分成两个四边形,求其中以点
分成两个四边形,求其中以点![]() 为顶点的四边形面积的最大值.
为顶点的四边形面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com