
分析 (Ⅰ)利用直角坐标方程与极坐标方程的转化方法,分别写出曲线C与直线l的极坐标方程;
(Ⅱ)由题意|OA|=4cosθ,|OB|=$\frac{12}{cosθ+\sqrt{3}sinθ}$,利用三角函数知识,可得结论.
解答 解:(Ⅰ)曲线C的方程为(x-2)2+y2=4,即x2+y2=4x,极坐标方程为ρ=4cosθ;
直线l的方程为x+$\sqrt{3}$y-12=0,极坐标方程为ρcosθ+$\sqrt{3}$ρsinθ-12=0;
(Ⅱ)由题意|OA|=4cosθ,|OB|=$\frac{12}{cosθ+\sqrt{3}sinθ}$,
∴$\frac{|OA|}{|OB|}$=$\frac{cosθ(cosθ+\sqrt{3}sinθ)}{3}$=$\frac{1}{6}$+$\frac{1}{3}$sin(2θ+$\frac{π}{6}$),
∵θ∈(0,$\frac{π}{2}$),∴2θ+$\frac{π}{6}$∈($\frac{π}{6}$,$\frac{7}{6}$π),
∴sin(2θ+$\frac{π}{6}$)∈(-$\frac{1}{2}$1],
∴$\frac{|OA|}{|OB|}$的最大值为$\frac{1}{2}$,此时$θ=\frac{π}{6}$.
点评 本题考查直角坐标方程与极坐标方程的转化,考查极坐标方程的运用,考查三角函数知识,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 3 | C. | 6 | D. | 7 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
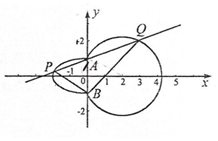 如图,曲线C由左半椭圆M:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0,x≤0)和圆N:(x-2)2+y2=5在y轴右侧的部分连接而成,A,B是M与N的公共点,点P,Q(均异于点A,B)分别是M,N上的动点.
如图,曲线C由左半椭圆M:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0,x≤0)和圆N:(x-2)2+y2=5在y轴右侧的部分连接而成,A,B是M与N的公共点,点P,Q(均异于点A,B)分别是M,N上的动点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com