
已知函数f(x)= x3-ax+1.
x3-ax+1.
(1)求x=1时,f(x)取得极值,求a的值;
(2)求f(x)在[0,1]上的最小值;
(3)若对任意m∈R,直线y=-x+m都不是曲线y=f(x)的切线,求a的取值范围.
(1)1 (2)见解析 (3)(-∞,-1)
【解析】(1)因为f′(x)=x2-a,
当x=1时,f(x)取得极值,所以f′(1)=1-a=0,a=1.
又当x∈(-1,1)时,f′(x)<0,x∈(1,+∞)时,f′(x)>0,
所以f(x)在x=1处取得极小值,即a=1符合题意.
(2)当a≤0时,f′(x)>0对x∈(0,1)成立,
所以f(x)在[0,1]上单调递增,f(x)在x=0处取最小值f(0)=1,
当a>0时,令f′(x)=x2-a=0,x1=- ,x2=
,x2= ,
,
当0<a<1时, <1,
<1,
x∈(0, )时,f′(x)<0,f(x)单调递减,
)时,f′(x)<0,f(x)单调递减,
x∈( ,1)时,f′(x)>0,f(x)单调递增,
,1)时,f′(x)>0,f(x)单调递增,
所以f(x)在x= 处取得最小值f(
处取得最小值f( )=1-
)=1- .
.
当a≥1时, ≥1,
≥1,
x∈[0,1]时,f′(x)<0,f(x)单调递减,
所以f(x)在x=1处取得最小值f(1)= -a.
-a.
综上所述,
当a≤0时,f(x)在x=0处取最小值f(0)=1;
当0<a<1时,f(x)在x= 处取得最小值f(
处取得最小值f( )=1-
)=1- ;
;
当a≥1时,f(x)在x=1处取得最小值f(1)= -a.
-a.
(3)因为?m∈R,直线y=-x+m都不是曲线y=f(x)的切线,
所以f′(x)=x2-a≠-1对x∈R成立,
只要f′(x)=x2-a的最小值大于-1即可,
而f′(x)=x2-a的最小值为f(0)=-a,
所以-a>-1,即a<1.
所以a的取值范围是(-∞,-1).


科目:高中数学 来源:2014年高考数学人教版评估检测 第二章 函数、导数及其应用(解析版) 题型:选择题
(能力挑战题)已知f(x)为R上的可导函数,且?x∈R,均有f(x)>f′(x),则有( )
A.e2014f(-2014)<f(0),f(2014)>e2014f(0)
B.e2014f(-2014)<f(0),f(2014)<e2014f(0)
C.e2014f(-2014)>f(0),f(2014)>e2014f(0)
D.e2014f(-2014)>f(0),f(2014)<e2014f(0)
查看答案和解析>>
科目:高中数学 来源:2014年高考数学人教版评估检测 第三章 三角函数、解三角形(解析版) 题型:选择题
(2014·随州模拟)已知函数f(x)=sin (x∈R),给出下面命题错误的是
(x∈R),给出下面命题错误的是
( )
A.函数f(x)的最小正周期为π
B.函数f(x)是偶函数
C.函数f(x)的图象关于直线x= 对称
对称
D.函数f(x)在区间 上是增函数
上是增函数
查看答案和解析>>
科目:高中数学 来源:2014年高考数学人教版评估检测 第七章 立体几何(解析版) 题型:填空题
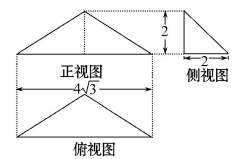
(2014·宁波模拟)已知某几何体的三视图如图所示,则该几何体的体积为________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学人教版评估检测 第七章 立体几何(解析版) 题型:选择题
(2014·宜昌模拟)一个直棱柱被一个平面截去一部分后所剩几何体的三视图如图所示,则该几何体的体积为( )

A.9 B.10 C.11 D.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学三轮冲刺模拟 集合、常用逻辑用语、不等式、函数与导数(解析版) 题型:解答题
已知集合A={y|y2-(a2+a+1)y+a(a2+1)>0},B={y|y= x2-x+
x2-x+ ,0≤x≤3}.
,0≤x≤3}.
(1)若A∩B=∅,求a的取值范围;
(2)当a取使不等式x2+1≥ax恒成立的a的最小值时,求(∁RA)∩B.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学三轮冲刺模拟 集合、常用逻辑用语、不等式、函数与导数(解析版) 题型:选择题
小王从甲地到乙地往返的时速分别为a和b(a<b),其全程的平均时速为v,则( )
A.a<v< B.v=
B.v=
C. <v<
<v< D.v=
D.v=
查看答案和解析>>
科目:高中数学 来源:2014年高考数学三轮冲刺模拟 解析几何(解析版) 题型:填空题
l1,l2是分别经过A(1,1),B(0,-1)两点的两条平行直线,当l1,l2间的距离最大时,直线l1的方程是________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学三轮冲刺模拟 概率与统计(解析版) 题型:填空题
从某小区抽取100户居民进行月用电量调查,发现其用电量都在50至350度之间,频率分布直方图如图所示.

(1)直方图中x的值为________;
(2)在这些用户中,用电量落在区间[100,250)内的户数为________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com