练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    (能力挑战题)已知f(x)为R上的可导函数,且?x∈R,均有f(x)>f′(x),则有(　　)

    A.e2014f(-2014)<f(0),f(2014)>e2014f(0)

    B.e2014f(-2014)<f(0),f(2014)<e2014f(0)

    C.e2014f(-2014)>f(0),f(2014)>e2014f(0)

    D.e2014f(-2014)>f(0),f(2014)<e2014f(0)

     

    D

    【解析】构造函数g(x)=,

    则g′(x)==.

    因为?x∈R,均有f(x)>f′(x),并且ex>0,

    所以g′(x)<0,故函数g(x)=在R上单调递减,

    所以g(-2014)>g(0),g(2014)<g(0),

    即>f(0),<f(0),

    也就是e2014f(-2014)>f(0),f(2014)<e2014f(0),故选D.

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：2014年高考数学人教版评估检测 第六章 不等式、推理与证明（解析版） 题型：填空题

    (2014·黄冈模拟)有纯农药液一桶,倒出8升后用水补满,然后又倒出4升后再用水补满,此时桶中的农药不超过容积的28%,问桶的容积最大为_______.

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学人教版评估检测 第五章 数列（解析版） 题型：填空题

    已知函数f(x)=2x,等差数列{an}的公差为2,若f(a2+a4+a6+a8+a10)=4,则log2[f(a1)·f(a2)·f(a3)·…·f(a10)]=________.

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学人教版评估检测 第二章 函数、导数及其应用（解析版） 题型：解答题

    (2014·成都模拟)已知函数f(x)=x2++alnx(x>0).

    (1)若f(x)在[1,+∞)上单调递增,求a的取值范围.

    (2)若定义在区间D上的函数y=f(x)对于区间D上的任意两个值x1,x2总有不等式[f(x1)+f(x2)]≥f成立,则称函数y=f(x)为区间D上的“凹函数”.试证当a≤0时,f(x)为“凹函数”.

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学人教版评估检测 第二章 函数、导数及其应用（解析版） 题型：填空题

    (2014·黄冈模拟)f(x)是定义在R上的偶函数,当x<0时,有f(x)+xf′(x)<0,且f(-4)=0,则不等式xf(x)>0的解集为________.

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学人教版评估检测 第二章 函数、导数及其应用（解析版） 题型：选择题

    (2014·宜昌模拟)若定义在R上的偶函数f(x)满足f(x+1)=-f(x),且在区间[0,1]上单调递减,则(　　)

    A.f(2)<f<f(1) B.f(1)<f(2)<f

    C.f<f(2)<f(1) D.f(1)<f<f(2)

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学人教版评估检测 第九章计数原理与概率随机变量及其分布（解析版） 题型：解答题

    (2014·黄冈模拟)某制造商3月生产了一批乒乓球,随机抽样100个进行检查,测得每个球的直径(单位：mm),将数据分组如表：

    分组

    频数

    频率

    [39.95,39.97)

    10

     

     

    [39.97,39.99)

    20

     

     

    [39.99,40.01)

    50

     

     

    [40.01,40.03]

    20

     

     

    合计

    100

     

     

     

    (1)请在上表中补充完成频率分布表(结果保留两位小数),并在图中画出频率分布直方图.

    (2)若以上述频率作为概率,已知标准乒乓球的直径为40.00mm,试求这批乒乓球的直径误差不超过0.03mm的概率.

    (3)统计方法中,同一组数据常用该组区间的中点值(例如,区间[39.99,40.01)的中点值是40.00)作为代表.据此估计这批乒乓球直径的平均值(结果保留两位小数).

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学人教版评估检测 第三章 三角函数、解三角形（解析版） 题型：解答题

    (2014·济南模拟)已知函数f(x)=sinωx-sin2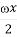+(ω>0)的最小正周期为π.

    (1)求ω的值及函数f(x)的单调递增区间.

    (2)当x∈时,求函数f(x)的取值范围.

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学三轮冲刺模拟 集合、常用逻辑用语、不等式、函数与导数（解析版） 题型：解答题

    已知函数f(x)＝x3－ax＋1.

    (1)求x＝1时，f(x)取得极值，求a的值；

    (2)求f(x)在[0,1]上的最小值；

    (3)若对任意m∈R，直线y＝－x＋m都不是曲线y＝f(x)的切线，求a的取值范围．

     

    查看答案和解析>>

    同步练习册答案