练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    (2014·黄冈模拟)f(x)是定义在R上的偶函数,当x<0时,有f(x)+xf′(x)<0,且f(-4)=0,则不等式xf(x)>0的解集为________.

     

    (-∞,-4)∪(0,4)

    【解析】因为[xf(x)]′=f(x)+xf′(x),根据已知条件可知,x<0时,

    [xf(x)]′<0,所以F(x)=xf(x)在(-∞,0)上递减,又因为f(x)是R上的偶函数,所以F(x)是R上的奇函数,则F(x)在(0,+∞)上递减,因为f(-4)=0,f(x)为R上的偶函数,所以f(4)=0,则F(-4)=F(4)=0,

    综合图象可知xf(x)>0的解集应为(-∞,-4)∪(0,4).

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：2014年高考数学人教版评估检测 第六章 不等式、推理与证明（解析版） 题型：解答题

    (2014·天津模拟)已知函数f(x)=x2+2x+a.

    (1)当a=时,求不等式f(x)>1的解集.

    (2)若对于任意x∈[1,+∞),f(x)>0恒成立,求实数a的取值范围.

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学人教版评估检测 第五章 数列（解析版） 题型：解答题

    (2014·随州模拟)已知等比数列{an}满足an+1+an=9·2n-1,n∈N*.

    (1)求数列{an}的通项公式.

    (2)设数列{an}的前n项和为Sn,若不等式Sn>kan-2对一切n∈N*恒成立,求实数k的取值范围.

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学人教版评估检测 第五章 数列（解析版） 题型：选择题

    已知数列{an}的前n项和Sn=n2-9n,第k项满足5<ak<8,则k等于(　　)

    A.9 B.8 C.7 D.6

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学人教版评估检测 第二章 函数、导数及其应用（解析版） 题型：解答题

    (2014·孝感模拟)已知定义在区间[0,2]上的两个函数f(x)和g(x),其中f(x)=-x2+2ax+1+a2,g(x)=x-+.

    (1)求函数f(x)的最小值.

    (2)对于?x1,x2∈[0,2],f(x1)>g(x2)恒成立,求实数a的取值范围.

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学人教版评估检测 第二章 函数、导数及其应用（解析版） 题型：选择题

    (能力挑战题)已知f(x)为R上的可导函数,且?x∈R,均有f(x)>f′(x),则有(　　)

    A.e2014f(-2014)<f(0),f(2014)>e2014f(0)

    B.e2014f(-2014)<f(0),f(2014)<e2014f(0)

    C.e2014f(-2014)>f(0),f(2014)>e2014f(0)

    D.e2014f(-2014)>f(0),f(2014)<e2014f(0)

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学人教版评估检测 第二章 函数、导数及其应用（解析版） 题型：选择题

    (2014·长沙模拟)某公司在甲、乙两地销售一种品牌车,利润(单位：万元)分别为L1=5.06x-0.15x2和L2=2x,其中x为销售量(单位：辆).若该公司在这两地共销售15辆车,则能获得的最大利润为(　　)

    A.45.606万元 B.45.6万元

    C.45.56万元 D.45.51万元

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学人教版评估检测 第九章计数原理与概率随机变量及其分布（解析版） 题型：选择题

    阅读程序框图,如果输出的函数值在区间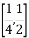内,那么输入的实数x的取值范围是(　　)

    A.(-∞,-2] B.[-2,-1] C.[-1,2] D.[2,+∞)

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学人教版评估检测 第七章 立体几何（解析版） 题型：选择题

    (2014·宜昌模拟)一个直棱柱被一个平面截去一部分后所剩几何体的三视图如图所示,则该几何体的体积为( )

    A.9 B.10 C.11 D.

     

    查看答案和解析>>

    同步练习册答案