
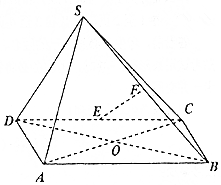
 如图,在四棱锥S-ABCD中,四边形ABCD是菱形,∠BAD=60°,AC交BC于点O,△SBD是边长为2的正三角形,SA=$\sqrt{3}$,E,F分别是CD,SB的中点.
如图,在四棱锥S-ABCD中,四边形ABCD是菱形,∠BAD=60°,AC交BC于点O,△SBD是边长为2的正三角形,SA=$\sqrt{3}$,E,F分别是CD,SB的中点.分析 (Ⅰ):取SA得中点为G,连接GD,GF,可得四边形DEFG为平行四边形,即可证得EF∥面SAD.
(Ⅱ)连接SO,只需证明SO⊥BO.,AC⊥BD.可证得BD⊥平面SAC.
(Ⅲ) 过A作AH⊥SO与H,可得ABH就是AB与平面SBD所成角.
在Rt△ABH中,sin$∠ABH=\frac{AH}{AB}=\frac{3}{4}$.即得直线AB与平面SBD所成角的正弦值为$\frac{3}{4}$.
解答 解:(Ⅰ)证明:取SA得中点为G,连接GD,GF,
∵E,F分别是CD,SB的中点.∴GF∥AB,GF=$\frac{1}{2}$AB,DE∥AB,DE=$\frac{1}{2}$AB.
∴GF∥DE,GF=DE,∴四边形DEFG为平行四边形.
∵DG?面SAD,EF?面SAD,∴EF∥面SAD.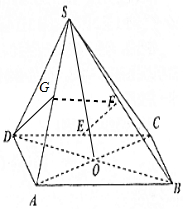
(Ⅱ)证明:连接SO,因为,△SBD是边长为2的正三角形,O为中点,∴SO⊥BO.
∵四边形ABCD是菱形,∴AC⊥BD.
又SO∩AC=O,∴BD⊥平面SAC.
(Ⅲ)如图2过A作AH⊥SO与H,由(Ⅱ)得面SAC⊥面SDB.
∴AH⊥面SDB,∴∠ABH就是AB与平面SBD所成角.
四边形ABCD是菱形,∠BAD=60°,△SBD是边长为2的正三角形,∴AB=2,AO=SO=$\sqrt{3}$,
∵SA=$\sqrt{3}$,∴△SAO是边长为$\sqrt{3}$的正三角形.
又因为AH⊥SO,∴H时SO得中点,∴AH=$\frac{3}{2}$,
在Rt△ABH中,sin$∠ABH=\frac{AH}{AB}=\frac{3}{4}$.
∴直线AB与平面SBD所成角的正弦值为$\frac{3}{4}$.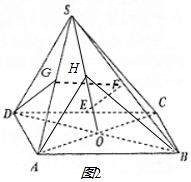
点评 本题考查了空间线面平行、垂直的判定,几何法求线面角,属于中档题,


 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {0,1,2,4} | B. | {2,3} | C. | {2,4} | D. | {0,4} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,0) | B. | (-∞,-$\frac{1}{2}$] | C. | [-$\frac{1}{2}$,0) | D. | (-∞,0)∪[2,+∞) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com