
| A. | (-∞,0) | B. | (-∞,-$\frac{1}{2}$] | C. | [-$\frac{1}{2}$,0) | D. | (-∞,0)∪[2,+∞) |
分析 画出约束条件的可行域,利用目标函数的最值判断最优解,利用直线的斜率求解即可.
解答 解:实数x,y满足约束条件$\left\{\begin{array}{l}{x≥1,}&{\;}\\{x+y≤4,}&{\;}\\{x+by-1≤0}&{\;}\end{array}\right.$的可行域如图: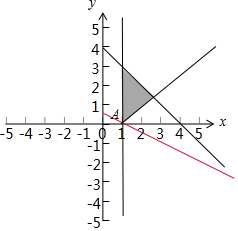
且目标函数z=x+2y最小值为1,可知目标函数经过可行域的A时,取得最小值,
由$\left\{\begin{array}{l}{x=1}\\{x+2y=1}\end{array}\right.$解得A(1,0),A在直线x+by-1=0上,可得-$\frac{1}{b}$$≥-\frac{1}{2}$,解得b≥2或b<0.
故选:D.
点评 本题考查线性规划的简单应用,直线的斜率的关系是解题的关键,考查计算能力.


 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案 走进文言文系列答案
走进文言文系列答案科目:高中数学 来源: 题型:解答题
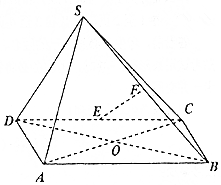 如图,在四棱锥S-ABCD中,四边形ABCD是菱形,∠BAD=60°,AC交BC于点O,△SBD是边长为2的正三角形,SA=$\sqrt{3}$,E,F分别是CD,SB的中点.
如图,在四棱锥S-ABCD中,四边形ABCD是菱形,∠BAD=60°,AC交BC于点O,△SBD是边长为2的正三角形,SA=$\sqrt{3}$,E,F分别是CD,SB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
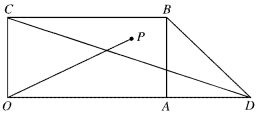 如图,已知矩形OABC中,OA=2,OC=1,OD=3,若P在△BCD中(包括边界),且$\overrightarrow{OP}$=α$\overrightarrow{OC}$+$\frac{1}{2}$β$\overrightarrow{OA}$,则α+$\frac{3}{2}$β的最大值为( )
如图,已知矩形OABC中,OA=2,OC=1,OD=3,若P在△BCD中(包括边界),且$\overrightarrow{OP}$=α$\overrightarrow{OC}$+$\frac{1}{2}$β$\overrightarrow{OA}$,则α+$\frac{3}{2}$β的最大值为( )| A. | $\frac{3}{2}$ | B. | $\frac{5}{2}$ | C. | $\frac{9}{2}$ | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
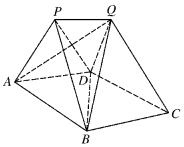 如图,P-ABD和Q-BCD为两个全等的正棱锥,且A,B,C,D四点共面,其中AB=1,∠APB=90°.
如图,P-ABD和Q-BCD为两个全等的正棱锥,且A,B,C,D四点共面,其中AB=1,∠APB=90°.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{9-2\sqrt{3}}{4}$ | B. | $\frac{11-3\sqrt{3}}{4}$ | C. | $\frac{13-4\sqrt{3}}{4}$ | D. | $\frac{15-5\sqrt{3}}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
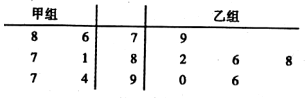 以下茎叶图记录了甲、乙两组各六名学生在一次数学测试中的成绩(单位:分),规定85分以上(含85分)为优秀,现分别从甲、乙两组中随机选取一名同学的数学成绩,则两人成绩都为优秀的概率是( )
以下茎叶图记录了甲、乙两组各六名学生在一次数学测试中的成绩(单位:分),规定85分以上(含85分)为优秀,现分别从甲、乙两组中随机选取一名同学的数学成绩,则两人成绩都为优秀的概率是( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{1}{4}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com