
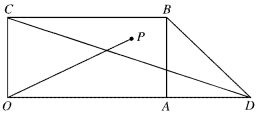
 如图,已知矩形OABC中,OA=2,OC=1,OD=3,若P在△BCD中(包括边界),且$\overrightarrow{OP}$=α$\overrightarrow{OC}$+$\frac{1}{2}$β$\overrightarrow{OA}$,则α+$\frac{3}{2}$β的最大值为( )
如图,已知矩形OABC中,OA=2,OC=1,OD=3,若P在△BCD中(包括边界),且$\overrightarrow{OP}$=α$\overrightarrow{OC}$+$\frac{1}{2}$β$\overrightarrow{OA}$,则α+$\frac{3}{2}$β的最大值为( )| A. | $\frac{3}{2}$ | B. | $\frac{5}{2}$ | C. | $\frac{9}{2}$ | D. | 3 |
分析 先建立以O为原点,以OD所在直线为x轴的直角坐标系,根据条件求出点P的坐标与α,β之间的关系,再根据点P的位置,借助于可行域即可求解.
解答 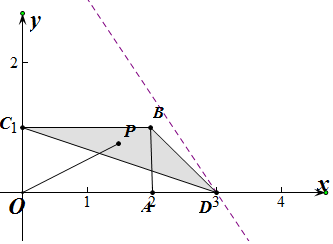 解:分别以边OA,OC所在直线为x,y轴建立如图所实施平面直角坐标系;
解:分别以边OA,OC所在直线为x,y轴建立如图所实施平面直角坐标系;
∴$\overrightarrow{OC}$=(0,1),$\overrightarrow{OD}$=(3,0),设$\overrightarrow{OP}$=(x,y),
∵$\overrightarrow{OP}$=α$\overrightarrow{OC}$+$\frac{1}{2}$β$\overrightarrow{OA}$,
∴(x,y)=α(0,1)+$\frac{1}{2}$β(2,0)=(β,α),
∴x=β,y=α,
设z=α+$\frac{3}{2}$β=y+$\frac{3}{2}$x,
所以z是直线y=-$\frac{3}{2}$x+z在y轴上的截距;
由图形可以看出,当该直线经过C(3,0)点时,它在y轴的截距z最大,最大为$\frac{9}{2}$;
∴α+$\frac{3}{2}$β的最大值是$\frac{9}{2}$.
故选:C
点评 本题考查通过建立平面直角坐标系,用向量坐标解决向量问题的方法,利用线性规划求最值的方法.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | {0,1,2,4} | B. | {2,3} | C. | {2,4} | D. | {0,4} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
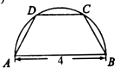 如图,将一块半径为2的半圆形纸板切割成等腰梯形的形状,下底AB是半圆的直径,上底CD的端点在半圆上,则所得梯形的最大面积为3$\sqrt{3}$.
如图,将一块半径为2的半圆形纸板切割成等腰梯形的形状,下底AB是半圆的直径,上底CD的端点在半圆上,则所得梯形的最大面积为3$\sqrt{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,0) | B. | (-∞,-$\frac{1}{2}$] | C. | [-$\frac{1}{2}$,0) | D. | (-∞,0)∪[2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com