
分析 (1)当a=b=c=1时,不等式f(x)>5即|x+1|+|x-1|+1>5,化为:|x+1|+|x-1|>4.对x与±1的大小关系分类讨论即可得出.
(2)不妨设a≥b>0.分类讨论:①x>b时,②-a≤x≤b时,③x<-a时,可知:-a≤x≤b时,f(x)取得最小值a+b+c=5.可得$\frac{1}{a}+\frac{1}{b}+\frac{1}{c}$=$\frac{1}{5}$(a+b+c)$(\frac{1}{a}+\frac{1}{b}+\frac{1}{c})$,再利用均值不等式的性质即可得出.
解答 解:(1)当a=b=c=1时,不等式f(x)>5即|x+1|+|x-1|+1>5,化为:|x+1|+|x-1|>4.
①x≥1时,化为:x+1+x-1>4,解得x>2.
②-1<x<1时,化为:x+1-(x-1)>4,化为:0>2,解得x∈∅.
③x≤-1时,化为:-(x+1)-(x-1)>4,化为:x<-2.
综上可得:不等式f(x)>5的解集为:(-∞,-2)∪(2,+∞).
(2)不妨设a≥b>0.
①x>b时,f(x)=x+a+x-b+c=2x+a-b+c,
②-a≤x≤b时,f(x)=a+x-(x-b)+c=a+b+c,
③x<-a时,f(x)=-(a+x)+b-x+c=-2x-a+b+c.
可知:-a≤x≤b时,f(x)取得最小值a+b+c=5.
∴$\frac{1}{a}+\frac{1}{b}+\frac{1}{c}$=$\frac{1}{5}$(a+b+c)$(\frac{1}{a}+\frac{1}{b}+\frac{1}{c})$≥$\frac{1}{5}×3\root{3}{abc}$×$3\root{3}{\frac{1}{a}×\frac{1}{b}×\frac{1}{c}}$=$\frac{9}{5}$,当且仅当a═b=c=$\frac{5}{3}$时取等号.
∴$\frac{1}{a}+\frac{1}{b}+\frac{1}{c}$的最小值为$\frac{9}{5}$.
点评 本题考查绝对值不等式的解法、均值不等式的性质、分类讨论方法,考查了推理能力与计算能力,属于中档题.


 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:高中数学 来源: 题型:解答题
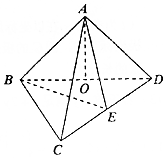 如图,在三棱锥A-BCD中,顶点A在底面BCD上的射影O在棱BD上,AB=AD=$\sqrt{2}$,BC=BD=2,∠CBD=90°,E为CD的中点.
如图,在三棱锥A-BCD中,顶点A在底面BCD上的射影O在棱BD上,AB=AD=$\sqrt{2}$,BC=BD=2,∠CBD=90°,E为CD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
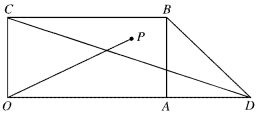 如图,已知矩形OABC中,OA=2,OC=1,OD=3,若P在△BCD中(包括边界),且$\overrightarrow{OP}$=α$\overrightarrow{OC}$+$\frac{1}{2}$β$\overrightarrow{OA}$,则α+$\frac{3}{2}$β的最大值为( )
如图,已知矩形OABC中,OA=2,OC=1,OD=3,若P在△BCD中(包括边界),且$\overrightarrow{OP}$=α$\overrightarrow{OC}$+$\frac{1}{2}$β$\overrightarrow{OA}$,则α+$\frac{3}{2}$β的最大值为( )| A. | $\frac{3}{2}$ | B. | $\frac{5}{2}$ | C. | $\frac{9}{2}$ | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{9-2\sqrt{3}}{4}$ | B. | $\frac{11-3\sqrt{3}}{4}$ | C. | $\frac{13-4\sqrt{3}}{4}$ | D. | $\frac{15-5\sqrt{3}}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
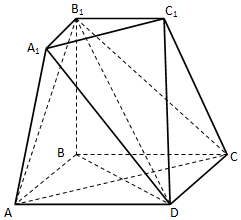 如图所示的几何体是由棱台ABC-A1B1C1和棱锥D-AA1C1C拼接而成的组合体,其底面四边形ABCD是边长为2的菱形,且∠BAD=60°,BB1⊥平面ABCD,BB1=2A1B1=2.(${V_{棱台}}=\frac{1}{3}h({{S_上}+{S_下}+\sqrt{{S_上}{S_下}}})$)
如图所示的几何体是由棱台ABC-A1B1C1和棱锥D-AA1C1C拼接而成的组合体,其底面四边形ABCD是边长为2的菱形,且∠BAD=60°,BB1⊥平面ABCD,BB1=2A1B1=2.(${V_{棱台}}=\frac{1}{3}h({{S_上}+{S_下}+\sqrt{{S_上}{S_下}}})$)查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(-\frac{1}{2},0)$ | B. | $(0,\frac{ln2+1}{4})$ | C. | $(\frac{1}{2},1)$ | D. | $(\frac{ln2+1}{4},\frac{1}{2})$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com