
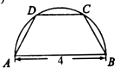
 如图,将一块半径为2的半圆形纸板切割成等腰梯形的形状,下底AB是半圆的直径,上底CD的端点在半圆上,则所得梯形的最大面积为3$\sqrt{3}$.
如图,将一块半径为2的半圆形纸板切割成等腰梯形的形状,下底AB是半圆的直径,上底CD的端点在半圆上,则所得梯形的最大面积为3$\sqrt{3}$. 分析 连接OD,过C,D分别作DE⊥AB于E,CF⊥AB,垂足分别为E,F.设∠AOD=θ$(θ∈(0,\frac{π}{2}))$.OE=2cosθ,DE=2sinθ.可得CD=2OE=4cosθ,梯形ABCD的面积S=$\frac{1}{2}(4+4cosθ)×2sinθ$=4sinθ(1+cosθ),利用导数研究函数的单调性极值与最值即可得出..
解答 解:连接OD,过C,D分别作DE⊥AB于E,CF⊥AB,垂足分别为E,F.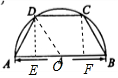
设∠AOD=θ$(θ∈(0,\frac{π}{2}))$.
OE=2cosθ,DE=2sinθ.
可得CD=2OE=4cosθ,
∴梯形ABCD的面积S=$\frac{1}{2}(4+4cosθ)×2sinθ$
=4sinθ(1+cosθ),
S′=4(cosθ+cos2θ-sin2θ)
=4(2cos2θ+cosθ-1)
=4(2cosθ-1)(cosθ+1).
∵θ∈$(0,\frac{π}{2})$,∴cosθ∈(0,1).
∴当cosθ=$\frac{1}{2}$即θ=$\frac{π}{3}$时,S取得最大值,S=3$\sqrt{3}$.
故最大值为:3$\sqrt{3}$.
点评 本题考查了换元法、利用导数研究函数的单调性极值与最值、梯形面积、三角函数基本关系式,考查了推理能力与计算能力,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | -462 | B. | 462 | C. | 792 | D. | -792 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
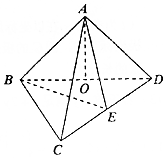 如图,在三棱锥A-BCD中,顶点A在底面BCD上的射影O在棱BD上,AB=AD=$\sqrt{2}$,BC=BD=2,∠CBD=90°,E为CD的中点.
如图,在三棱锥A-BCD中,顶点A在底面BCD上的射影O在棱BD上,AB=AD=$\sqrt{2}$,BC=BD=2,∠CBD=90°,E为CD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
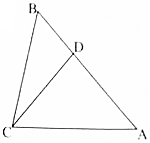
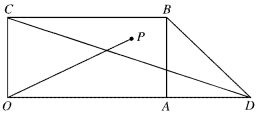 如图,已知矩形OABC中,OA=2,OC=1,OD=3,若P在△BCD中(包括边界),且$\overrightarrow{OP}$=α$\overrightarrow{OC}$+$\frac{1}{2}$β$\overrightarrow{OA}$,则α+$\frac{3}{2}$β的最大值为( )
如图,已知矩形OABC中,OA=2,OC=1,OD=3,若P在△BCD中(包括边界),且$\overrightarrow{OP}$=α$\overrightarrow{OC}$+$\frac{1}{2}$β$\overrightarrow{OA}$,则α+$\frac{3}{2}$β的最大值为( )| A. | $\frac{3}{2}$ | B. | $\frac{5}{2}$ | C. | $\frac{9}{2}$ | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{9-2\sqrt{3}}{4}$ | B. | $\frac{11-3\sqrt{3}}{4}$ | C. | $\frac{13-4\sqrt{3}}{4}$ | D. | $\frac{15-5\sqrt{3}}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(-\frac{1}{2},0)$ | B. | $(0,\frac{ln2+1}{4})$ | C. | $(\frac{1}{2},1)$ | D. | $(\frac{ln2+1}{4},\frac{1}{2})$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com