
分析 根据题意,由双曲线的方程可得a、b,计算可得c的值,进而有双曲线的渐近线、离心率公式计算可得答案.
解答 解:根据题意,双曲线的方程为$\frac{x^2}{3}-\frac{y^2}{6}=1$,
其中a=$\sqrt{3}$,b=$\sqrt{6}$,则c=$\sqrt{6+3}$=3,
又由其焦点在x轴上,则其渐近线方程为:y=±$\sqrt{2}$x,
其离心率e=$\frac{c}{a}$=$\frac{3}{\sqrt{3}}$=$\sqrt{3}$;
故答案为:y=±$\sqrt{2}$x,$\sqrt{3}$.
点评 本题考查双曲线的标准方程,关键要熟悉双曲线标准方程的形式.


科目:高中数学 来源: 题型:选择题
| A. | 10 | B. | 11 | C. | 12 | D. | 13 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 18 | B. | 24 | C. | 30 | D. | 60 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 从某市的中学生中随机调查了部分男生,获得了他们的身高数据,整理得到如下频率分布直方图.
从某市的中学生中随机调查了部分男生,获得了他们的身高数据,整理得到如下频率分布直方图.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 年份 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 |
| t | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| y | 270 | 330 | 390 | 450 | 490 | 540 | 610 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
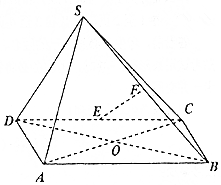 如图,在四棱锥S-ABCD中,四边形ABCD是菱形,∠BAD=60°,AC交BC于点O,△SBD是边长为2的正三角形,SA=$\sqrt{3}$,E,F分别是CD,SB的中点.
如图,在四棱锥S-ABCD中,四边形ABCD是菱形,∠BAD=60°,AC交BC于点O,△SBD是边长为2的正三角形,SA=$\sqrt{3}$,E,F分别是CD,SB的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com