
分析 (1)利用导数求出斜率,再用点斜式写出方程;
(2)构造函数h(x)=ax3-f(x)=ax3-sinx+xcosx,
h′(x)=x(3ax-sinx),可得a≥$\frac{1}{3}$,则?x∈[0,$\frac{π}{2}$],cosx≤1,∴G′(x)=3a-cosx≥0在[0,$\frac{π}{2}$]恒成立,
即h(x)≥h(0)=0,得到a≥$\frac{1}{3}$,则?x∈[0,$\frac{π}{2}$],不等式f(x)≤ax3恒成立.
(3)求出m,.可得g(x)=$\frac{6m}{(4-π){x}^{2}}$f(x)=$\frac{3}{{x}^{2}}f(x)$.
利用x$∈(0,\frac{π}{2})$时,tanx>x,及(2)得x$∈(0,\frac{π}{2})$时,f(x)$<\frac{1}{3}{x}^{2}$,即0$<g(\frac{1}{{3}^{n}})<\frac{1}{{3}^{n}}$
利用x>0时,x+1<ex,得x>0时,0$<1+g(\frac{1}{{3}^{n}})<1+\frac{1}{{3}^{n}}<{e}^{\frac{1}{{3}^{n}}}$;
[1+g($\frac{1}{3}$)][1+g($\frac{1}{{3}^{2}}$)][1+g($\frac{1}{{3}^{3}}$)]…[1+g($\frac{1}{{3}^{n}}$)]<${e}^{\frac{1}{3}}•{e}^{\frac{1}{{3}^{2}}}•{e}^{\frac{1}{{3}^{3}}}…{e}^{\frac{1}{{3}^{n}}}$=${e}^{\frac{1}{3}+\frac{1}{{3}^{2}}+…+\frac{1}{{3}^{n}}}$得证
解答 解:(1)f′(x)=cosx-(cosx-xsinx)=xsinx,
∴f′($\frac{π}{2}$)=$\frac{π}{2}$,函数f(x)的图象在($\frac{π}{2}$,1)处的切线方程为y-1=$\frac{π}{2}(x-\frac{π}{2})$,
即y=$\frac{π}{2}x-\frac{{π}^{2}}{4}+1$为所求.
(2)a≥$\frac{1}{3}$,?x∈[0,$\frac{π}{2}$],不等式f(x)≤ax3恒成立.
理由:令h(x)=ax3-f(x)=ax3-sinx+xcosx,
h′(x)=x(3ax-sinx),
令G(x)=3ax-sinx,G′(x)=3a-cosx,
∵a≥$\frac{1}{3}$,则?x∈[0,$\frac{π}{2}$],cosx≤1,∴G′(x)=3a-cosx≥0在[0,$\frac{π}{2}$]恒成立,
∴G(x在[0,$\frac{π}{2}$]递增,∴G(x)≥G(0)=0,故h′(x)=x(3ax-sinx)≥0,
∴h(x)在[0,$\frac{π}{2}$]递增,∴h(x)≥h(0)=0,
∴a≥$\frac{1}{3}$,则?x∈[0,$\frac{π}{2}$],不等式f(x)≤ax3是恒成立.
(3)证明:∵(-2cosx-xsinx)′=sinx-xcosx=f(x).
∴m=${∫}_{0}^{\frac{π}{2}}$f(x)dx=-$\frac{π}{2}$+2.∴g(x)=$\frac{6m}{(4-π){x}^{2}}$f(x)=$\frac{3}{{x}^{2}}f(x)$.
∵x$∈(0,\frac{π}{2})$时,tanx>x,即sinx>xcosx,故g(x)>0,
由(2)得x$∈(0,\frac{π}{2})$时,f(x)$<\frac{1}{3}{x}^{2}$,
∴0<g(x)<x,即0$<g(\frac{1}{{3}^{n}})<\frac{1}{{3}^{n}}$
易得x>0时,x+1<ex
∴x>0时,0$<1+g(\frac{1}{{3}^{n}})<1+\frac{1}{{3}^{n}}<{e}^{\frac{1}{{3}^{n}}}$;
所以[1+g($\frac{1}{3}$)][1+g($\frac{1}{{3}^{2}}$)][1+g($\frac{1}{{3}^{3}}$)]…[1+g($\frac{1}{{3}^{n}}$)]<${e}^{\frac{1}{3}}•{e}^{\frac{1}{{3}^{2}}}•{e}^{\frac{1}{{3}^{3}}}…{e}^{\frac{1}{{3}^{n}}}$=${e}^{\frac{1}{3}+\frac{1}{{3}^{2}}+…+\frac{1}{{3}^{n}}}$
∵$\frac{1}{3}+\frac{1}{{3}^{2}}+\frac{1}{{3}^{2}}+…+\frac{1}{{3}^{n}}=\frac{1}{2}(1-\frac{1}{{3}^{n}})<\frac{1}{2}$,
∴[1+g($\frac{1}{3}$)][1+g($\frac{1}{{3}^{2}}$)][1+g($\frac{1}{{3}^{3}}$)]…[1+g($\frac{1}{{3}^{n}}$)]<$\sqrt{e}$
点评 本题考查了导数的几何意义,函数不等式的证明、函数不等式的放缩,属于难题.


科目:高中数学 来源: 题型:选择题
| A. | {-1,0,1} | B. | {0,1,2} | C. | {0,1,2,3} | D. | {-1,0,1,2,3} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
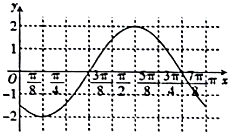 函数f(x)=Asin(ωx+φ)(ω>0,$|φ|<\frac{π}{2}$)的部分图象如图所示,将函数f(x)的图象向右平移$\frac{7π}{24}$个单位后得到函数g(x)的图象,若函数g(x)在区间$[{-\frac{π}{3},θ}]$($θ>-\frac{π}{3}$)上的值域为[-1,2],则θ等于( )
函数f(x)=Asin(ωx+φ)(ω>0,$|φ|<\frac{π}{2}$)的部分图象如图所示,将函数f(x)的图象向右平移$\frac{7π}{24}$个单位后得到函数g(x)的图象,若函数g(x)在区间$[{-\frac{π}{3},θ}]$($θ>-\frac{π}{3}$)上的值域为[-1,2],则θ等于( )| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{2π}{3}$ | D. | $\frac{7π}{12}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
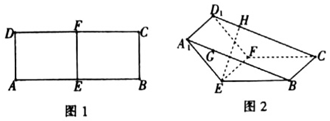 如图1,在矩形ABCD中,AB=8,AD=3,点E、F分别为AB、CD的中点,将四边形AEFD沿EF折到A1EFD1的位置,使∠A1EB=120°,如图2所示,点G,H分别在A1B,D1C上,A1G=D1H=$\sqrt{3}$,过点G,H的平面α与几何体A1EB-D1FC的面相交,交线围成一个正方形.
如图1,在矩形ABCD中,AB=8,AD=3,点E、F分别为AB、CD的中点,将四边形AEFD沿EF折到A1EFD1的位置,使∠A1EB=120°,如图2所示,点G,H分别在A1B,D1C上,A1G=D1H=$\sqrt{3}$,过点G,H的平面α与几何体A1EB-D1FC的面相交,交线围成一个正方形.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com