练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    10．（x2-$\frac{2}{x}$+y）5的展开式中，含x3y2的项的系数为（　　）
    A．60B．-60C．80D．-80

    分析 根据乘方的意义，求得x3y2的项的系数．

    解答 解：由于（x2-$\frac{2}{x}$+y）5的表示5个因式（x2-$\frac{2}{x}$+y）的乘积，故其中有2个因式取y，2个因式取x2，一个因式取-$\frac{2}{x}$，
    可得含x3y2的项，故含x3y2的项的系数为${C}_{5}^{2}$•${C}_{3}^{2}$•${C}_{1}^{1}$•（-2）=-60，
    故选：B．

    点评 本题主要考查二项式定理的应用，乘方的意义，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

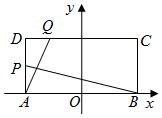    20．如图，在矩形ABCD中，|AB|=4，|AD|=2，O为AB中点，P，Q分别是AD和CD上的点，且满足①$\frac{|AP|}{|AD|}$=$\frac{|DQ|}{|DC|}$，②直线AQ与BP的交点在椭圆E：$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1（a＞b＞0）上．
    （Ⅰ）求椭圆E的方程；
    （Ⅱ）设R为椭圆E的右顶点，M为椭圆E第一象限部分上一点，作MN垂直于y轴，垂足为N，求梯形ORMN面积的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    1．已知集合A={y|0≤y＜2，y∈N}，B={x|x2-4x-5≤0，x∈N}，则A∩B=（　　）
    A．{1}B．{0，1}C．[0，2）D．∅

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

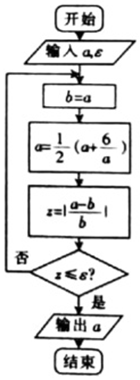    18．十七世纪英国著名数学家、物理学家牛顿创立的求方程近似解的牛顿迭代法，相较于二分法更具优势，如图给出的是利用牛顿迭代法求方程x2=6的正的近似解的程序框图，若输入a=2，?=0.02，则输出的结果为（　　）
    A．3B．2.5C．2.45D．2.4495

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    5．已知f（x）=sinx-xcosx（x≥0）．
    （1）求函数f（x）的图象在（$\frac{π}{2}$，1）处的切线方程；
    （2）若a≥$\frac{1}{3}$，则?x∈[0，$\frac{π}{2}$]，不等式f（x）≤ax3是否恒成立？并说明你的理由．
    （3）若m=${∫}_{0}^{\frac{π}{2}}$f（x）dx，g（x）=$\frac{6m}{（4-π）{x}^{2}}$f（x），证明：[1+g（$\frac{1}{3}$）][1+g（$\frac{1}{{3}^{2}}$）][1+g（$\frac{1}{{3}^{3}}$）]…[1+g（$\frac{1}{{3}^{n}}$）]＜$\sqrt{e}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    15．已知函数f（x）=2|x-2|+3|x+3|．
    （1）解不等式：f（x）＞15；
    （2）若函数f（x）的最小值为m，正实数a，b满足4a+25b=m，证明：$\frac{1}{a}$+$\frac{1}{b}$≥$\frac{49}{10}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    2．关于x的方程$（{k-7}）{x^2}+4lnx-\frac{1}{x^2}+k=0$有两个不等实根，则实数k的取值范围是（4，7）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    19．从某市的中学生中随机调查了部分男生，获得了他们的身高数据，整理得到如下频率分布直方图．
    （Ⅰ）求a的值；
    （Ⅱ）假设同组中的每个数据用该组区间的中点值代替，估计该市中学生中的全体男生的平均身高；
    （Ⅲ）从该市的中学生中随机抽取一名男生，根据直方图中的信息，估计其身高在180cm 以上的概率．若从全市中学的男生（人数众多）中随机抽取3人，用X表示身高在180cm以上的男生人数，求随机变量X的分布列和数学期望EX．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    20．若${（x-\frac{1}{x}）}^{n}$的展开式中只有第7项的二项式系数最大，则展开式中含x2项的系数是（　　）
    A．-462B．462C．792D．-792

    查看答案和解析>>

    同步练习册答案