
分析 (Ⅰ)求出导函数$f'(x)=\frac{1}{x}-\frac{1}{x^2}=\frac{x-1}{x^2}$(x>0).求出函数的最小值,利用二次函数的性质推出结果.
(Ⅱ)记当x≥0时,g(x)的最小值为g(x)min,当x>0时,[f(x)]的最小值为[f(x)]min,题目转化为g(x)min≥[f(x)]min,h(x)=ex-x-a,h'(x)=ex-1,通过求解导数,①当a≤1时,求出$g{(x)_{min}}=1-\frac{a^2}{2}≥0$,②当a>1时,利用h(x)在[0,+∞)上是增函数,推出$a={e^{x_0}}-{x_0}$,转化求出$g{(x)_{min}}=g({x_0})={e^{x_0}}-\frac{1}{2}{x_0}-a{x_0}-\frac{1}{2}{a^2}≥0$,转化求解1<a≤2-ln2.
解答 解:(Ⅰ)$f'(x)=\frac{1}{x}-\frac{1}{x^2}=\frac{x-1}{x^2}$(x>0).
当x>1时,f'(x)>0,当0<x<1时,f'(x)<0,
即f(x)在(0,1)上单调递减,在(1,+∞)上单调递增,
所以,当x=1时,f(x)取得最小值,最小值为$f(1)=\frac{1}{2}$,
所以$|f(x)|=f(x)≥\frac{1}{2}$,
又$-{(x-1)^2}+\frac{1}{2}≤\frac{1}{2}$,且当x=1时等号成立,
所以,$|f(x)|≥-{(x-1)^2}+\frac{1}{2}$.
(Ⅱ)记当x≥0时,g(x)的最小值为g(x)min,当x>0时,[f(x)]的最小值为[f(x)]min,
依题意有g(x)min≥[f(x)]min,
由(Ⅰ)知$f(x)≥\frac{1}{2}$,所以[f(x)]min=0,则有g(x)min≥0,g'(x)=ex-x-a.
令h(x)=ex-x-a,h'(x)=ex-1,
而当x≥0时,ex≥1,所以h'(x)≥0,
所以h(x)在[0,+∞)上是增函数,所以h(x)min=h(0)=1-a.
①当1-a≥0,即a≤1时,h(x)≥0恒成立,即g'(x)≥0,
所以g(x)在[0,+∞)上是增函数,所以$g{(x)_{min}}=g(0)=1-\frac{a^2}{2}$,
依题意有$g{(x)_{min}}=1-\frac{a^2}{2}≥0$,解得$-\sqrt{2}≤a≤\sqrt{2}$,
所以$-\sqrt{2}≤a≤1$.
②当1-a<0,即a>1时,因为h(x)在[0,+∞)上是增函数,且h(0)=1-a<0,
若a+2<e2,即1<a<e2-2,则h(ln(a+2))=a+2-ln(a+2)-a=2-ln(a+2)>0,
所以?x0∈(0,ln(a+2)),使得h(x0)=0,即$a={e^{x_0}}-{x_0}$,
且当x∈(0,x0)时,h(x)<0,即g'(x)<0;当x∈(x0,+∞)时,h(x)>0,即g'(x)>0,
所以,g(x)在(0,x0)上是减函数,在(x0,+∞)上是增函数,
所以$g{(x)_{min}}=g({x_0})={e^{x_0}}-\frac{1}{2}{x_0}-a{x_0}-\frac{1}{2}{a^2}≥0$,
又$a={e^{x_0}}-{x_0}$,所以$g{(x)_{min}}={e^{x_0}}-\frac{1}{2}{({x_0}+a)^2}={e^{x_0}}-\frac{1}{2}{e^{2{x_0}}}=\frac{1}{2}{e^{x_0}}(2-{e^{x_0}})≥0$,
所以${e^{x_0}}≤2$,所以0<x0≤ln2.
由$a={e^{x_0}}-{x_0}$,可令t(x)=ex-x,t'(x)=ex-1,当x∈(0,ln2]时,ex>1,所以t(x)在(0,ln2]上是增函数,
所以当x∈(0,ln2]时,t(0)<t(x)≤t(ln2),即1<t(x)≤2-ln2,
所以1<a≤2-ln2.
综上,所求实数a的取值范围是$[{-\sqrt{2},2-ln2}]$.
点评 本题考查函数的导数的综合应用,函数的极值以及函数的最值的应用,考查分析问题解决问题的能力,转化思想的应用.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
 秦九韶是我国南宋时期的数学家,他在《数学九章》中提出的多项式的秦九韶算法,至今仍是比较先进的算法,如图是事项该算法的程序框图,执行该程序框图,若输入n,x的值分别为4,2,则输出v的值为( )
秦九韶是我国南宋时期的数学家,他在《数学九章》中提出的多项式的秦九韶算法,至今仍是比较先进的算法,如图是事项该算法的程序框图,执行该程序框图,若输入n,x的值分别为4,2,则输出v的值为( )| A. | 5 | B. | 12 | C. | 25 | D. | 50 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
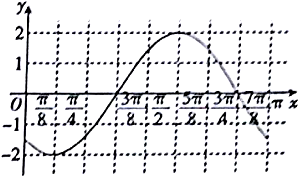 函数f(x)=Asin(ωx+φ)(ω>0,$|φ|<\frac{π}{2}$)的部分图象如图所示,将函数f(x)的图象向右平移$\frac{7π}{24}$个单位后得到函数g(x)的图象,若函数g(x)在区间$[{-\frac{π}{3},θ}]$($θ>-\frac{π}{3}$)上的值域为[-1,2],则θ=$\frac{π}{4}$.
函数f(x)=Asin(ωx+φ)(ω>0,$|φ|<\frac{π}{2}$)的部分图象如图所示,将函数f(x)的图象向右平移$\frac{7π}{24}$个单位后得到函数g(x)的图象,若函数g(x)在区间$[{-\frac{π}{3},θ}]$($θ>-\frac{π}{3}$)上的值域为[-1,2],则θ=$\frac{π}{4}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
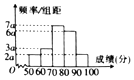 已知在一次全国数学竞赛中,某市3000名参赛学生的初赛成绩统计如图所示.
已知在一次全国数学竞赛中,某市3000名参赛学生的初赛成绩统计如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 18 | B. | 24 | C. | 30 | D. | 60 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com