
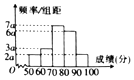
 ��֪��һ��ȫ����ѧ�����У�ij��3000������ѧ���ij����ɼ�ͳ����ͼ��ʾ��
��֪��һ��ȫ����ѧ�����У�ij��3000������ѧ���ij����ɼ�ͳ����ͼ��ʾ������ ��1��������ɵã���2a+2a+3a+6a+7a����10=1�����a��
��2��70+$\frac{5}{7}����80-70��$=$\frac{540}{7}$��
��3�����гɼ���80�����ϣ���80�֣��ĸ���P=$\frac{2a+6a}{20a}$=$\frac{2}{5}$���ɵ�X��B$��4��\frac{2}{5}��$�����ɵó�X�ķֲ�������ѧ������
��� �⣺��1��������ɵã���2a+2a+3a+6a+7a����10=1�����a=0.005��
��ɼ��ڵ�[80��90���ϵ�ѧ������=6��0.005��10��3000=900��
��2��70+$\frac{5}{7}����80-70��$=$\frac{540}{7}$��
���Գɼ����ڻ����$\frac{540}{7}$�Ľ��������
��3�����гɼ���80�����ϣ���80�֣��ĸ���P=$\frac{2a+6a}{20a}$=$\frac{2}{5}$����X��B$��4��\frac{2}{5}��$��
��P��X=k��=${∁}_{4}^{k}��\frac{2}{5}��^{k}��\frac{3}{5}��^{4-k}$���ɵ�P��X=0��=$\frac{81}{625}$��P��X=1��=$\frac{216}{625}$��P��X=2��=$\frac{216}{625}$��P��X=3��=$\frac{96}{625}$��P��X=4��=$\frac{16}{625}$��
��X�ķֲ���Ϊ��
| X | 0 | 1 | 2 | 3 | 4 |
| P | $\frac{81}{625}$ | $\frac{216}{625}$ | $\frac{216}{625}$ | $\frac{96}{625}$ | $\frac{16}{625}$ |
���� ���⿼���˶���ֲ��м�����ѧ������Ƶ�ʷֲ�ֱ��ͼ�����ʣ�������������������������������е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -2014 | B�� | -2015 | C�� | -2016 | D�� | -2017 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
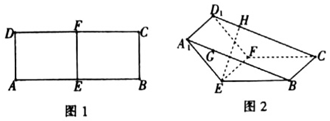 ��ͼ1���ھ���ABCD�У�AB=8��AD=3����E��F�ֱ�ΪAB��CD���е㣬���ı���AEFD��EF�۵�A1EFD1��λ�ã�ʹ��A1EB=120�㣬��ͼ2��ʾ����G��H�ֱ���A1B��D1C�ϣ�A1G=D1H=$\sqrt{3}$������G��H��ƽ����뼸����A1EB-D1FC�����ཻ������Χ��һ�������Σ�
��ͼ1���ھ���ABCD�У�AB=8��AD=3����E��F�ֱ�ΪAB��CD���е㣬���ı���AEFD��EF�۵�A1EFD1��λ�ã�ʹ��A1EB=120�㣬��ͼ2��ʾ����G��H�ֱ���A1B��D1C�ϣ�A1G=D1H=$\sqrt{3}$������G��H��ƽ����뼸����A1EB-D1FC�����ཻ������Χ��һ�������Σ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 8 | B�� | 10 | C�� | 12 | D�� | 16 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 0 | B�� | $\frac{2}{3}$ | C�� | -1 | D�� | $\frac{1}{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
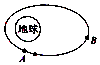 ������ŷɴ��ɹ�����˵�һ�����˺�����У�ʵ�����й�����ĺ������룬ij��ʱ��ɴ���̫�������еĹ����һ����Բ����������Բ��һ�������ϣ���ͼ��ʾ�����躽��Ա�������������Ϊd1����������Զ����Ϊd2������İ뾶ΪR�������������һ��������������������۷ɴ����й��������һ�������ϣ�����ס��һ�����ɷ���ij�������ź���Ҫ�����еĺ���Ա��ת������˲��ܽ��յ����������źŴ�������̾���Ϊ��������
������ŷɴ��ɹ�����˵�һ�����˺�����У�ʵ�����й�����ĺ������룬ij��ʱ��ɴ���̫�������еĹ����һ����Բ����������Բ��һ�������ϣ���ͼ��ʾ�����躽��Ա�������������Ϊd1����������Զ����Ϊd2������İ뾶ΪR�������������һ��������������������۷ɴ����й��������һ�������ϣ�����ס��һ�����ɷ���ij�������ź���Ҫ�����еĺ���Ա��ת������˲��ܽ��յ����������źŴ�������̾���Ϊ��������| A�� | d1+d2+R | B�� | d2-d1+2R | C�� | d2+d1-2R | D�� | d1+d2 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com