
分析 (Ⅰ)由b=1,由∠F1BO=60°,则a=2.即可求得椭圆W的标准方程;
(Ⅱ)由题意设N和E点坐标,设直线AE的方程,当y=-1,即可求得C点坐标,求得G点坐标,则$\overrightarrow{OE}=(\frac{x_0}{2},{y_0})$,$\overrightarrow{GE}=(\frac{x_0}{2}-\frac{x_0}{{2(1-{y_0})}},{y_0}+1)$.根据向量数量积的坐标运算,即可求得$\overrightarrow{OE}$•$\overrightarrow{GE}$=0,则$\overrightarrow{OE}⊥\overrightarrow{GE}$,则∠OEG=90°.
解答 解:(Ⅰ)依题意,得b=1.又∠F1BF2=120°,
在Rt△BF1O中,∠F1BO=60°,则a=2.
∴椭圆W的标准方程为$\frac{x^2}{4}+{y^2}=1$. …(4分)
(Ⅱ)设M(x0,y0),x0≠0,则N(0,y0),E$(\frac{x_0}{2},{y_0})$.
由点M在椭圆W上,则$\frac{{{x_0}^2}}{4}+{y_0}^2=1$.即${x_0}^2=4-4{y_0}^2$.
又A(0,1),则直线AE的方程为$y-1=\frac{{2({y_0}-1)}}{x_0}x$.
令y=-1,得C$(\frac{x_0}{{1-{y_0}}},-1)$.
又B(0,-1),G为线段BC的中点,则G$(\frac{x_0}{{2(1-{y_0})}},-1)$.
∴$\overrightarrow{OE}=(\frac{x_0}{2},{y_0})$,$\overrightarrow{GE}=(\frac{x_0}{2}-\frac{x_0}{{2(1-{y_0})}},{y_0}+1)$.
∵$\overrightarrow{OE}•\overrightarrow{GE}=\frac{x_0}{2}(\frac{x_0}{2}-\frac{x_0}{{2(1-{y_0})}})+{y_0}({y_0}+1)$=$\frac{{{x_0}^2}}{4}-\frac{{{x_0}^2}}{{4(1-{y_0})}}+{y_0}^2+{y_0}$
=$1-\frac{{4-4{y_0}^2}}{{4(1-{y_0})}}+{y_0}$=1-y0-1+y0=0,
∴$\overrightarrow{OE}⊥\overrightarrow{GE}$.则∠OEG=90°,
∠OEG为90°. …(13分)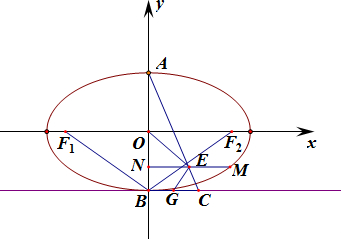
点评 本题考查椭圆的标准方程,直线的点斜式方程,向量数量积的坐标运算,考查计算能力,属于中档题.


 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
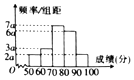 已知在一次全国数学竞赛中,某市3000名参赛学生的初赛成绩统计如图所示.
已知在一次全国数学竞赛中,某市3000名参赛学生的初赛成绩统计如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 18 | B. | 24 | C. | 30 | D. | 60 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 30° | B. | 60° | C. | 150° | D. | 120° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com