
| A. | 30° | B. | 60° | C. | 150° | D. | 120° |
分析 先根据余弦定理以及三角的面积公式可得sinA=$\sqrt{3}$(cosA+1),再根据cos2A+sin2A=1,即可求出答案
解答 解:∵a2=(b+c)2-4=b2+c2+2bc-4,
∴cosA=$\frac{{b}^{2}+{c}^{2}-{a}^{2}}{2bc}$=$\frac{4-2bc}{2bc}$=$\frac{2}{bc}$-1
∵△ABC的面积为$\sqrt{3}$,
∴$\frac{1}{2}$bcsinA=$\sqrt{3}$,
∴bc=$\frac{2\sqrt{3}}{sinA}$,
∴cosA=$\frac{2}{\frac{2\sqrt{3}}{sinA}}$-1=$\frac{\sqrt{3}}{3}$sinA-1,
∴sinA=$\sqrt{3}$(cosA+1)
∵cos2A+sin2A=1,
∴3(cosA+1)2+cos2A=1,
∴4cos2A+6cosA+2=0
(2cosA+1)(cosA+1)=0,
∵cosA+1≠0
∴cosA=-$\frac{1}{2}$,
∴A=120°,
故选:D.
点评 本题考查了三角函数的化简和余弦定理和三角形的面积公式,考查了学生的运算能力,属于中档题


 出彩同步大试卷系列答案
出彩同步大试卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
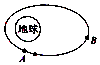 神舟五号飞船成功完成了第一次载人航天飞行,实现了中国人民的航天梦想,某段时间飞船在太空中运行的轨道是一个椭圆,地球在椭圆的一个焦点上,如图所示,假设航天员到地球最近距离为d1,到地球最远距离为d2,地球的半径为R,我们想象存在一个镜像地球,其中心在神舟飞船运行轨道的另外一个焦点上,上面住着一个神仙发射某种神秘信号需要飞行中的航天员中转后地球人才能接收到,则神秘信号传导的最短距离为( )
神舟五号飞船成功完成了第一次载人航天飞行,实现了中国人民的航天梦想,某段时间飞船在太空中运行的轨道是一个椭圆,地球在椭圆的一个焦点上,如图所示,假设航天员到地球最近距离为d1,到地球最远距离为d2,地球的半径为R,我们想象存在一个镜像地球,其中心在神舟飞船运行轨道的另外一个焦点上,上面住着一个神仙发射某种神秘信号需要飞行中的航天员中转后地球人才能接收到,则神秘信号传导的最短距离为( )| A. | d1+d2+R | B. | d2-d1+2R | C. | d2+d1-2R | D. | d1+d2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com