
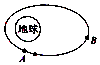
 神舟五号飞船成功完成了第一次载人航天飞行,实现了中国人民的航天梦想,某段时间飞船在太空中运行的轨道是一个椭圆,地球在椭圆的一个焦点上,如图所示,假设航天员到地球最近距离为d1,到地球最远距离为d2,地球的半径为R,我们想象存在一个镜像地球,其中心在神舟飞船运行轨道的另外一个焦点上,上面住着一个神仙发射某种神秘信号需要飞行中的航天员中转后地球人才能接收到,则神秘信号传导的最短距离为( )
神舟五号飞船成功完成了第一次载人航天飞行,实现了中国人民的航天梦想,某段时间飞船在太空中运行的轨道是一个椭圆,地球在椭圆的一个焦点上,如图所示,假设航天员到地球最近距离为d1,到地球最远距离为d2,地球的半径为R,我们想象存在一个镜像地球,其中心在神舟飞船运行轨道的另外一个焦点上,上面住着一个神仙发射某种神秘信号需要飞行中的航天员中转后地球人才能接收到,则神秘信号传导的最短距离为( )| A. | d1+d2+R | B. | d2-d1+2R | C. | d2+d1-2R | D. | d1+d2 |
分析 设椭圆的方程,根据题意可得:$\left\{\begin{array}{l}{{d}_{1}+R=a-c}\\{{d}_{2}+R=a+c}\end{array}\right.$,则2a=d1+d2+2R,利用椭圆的定义可知神秘信号的最短距离为丨PF1丨+丨PF2丨-2R=2a-2R=d1+d2.
解答 解:设椭圆的方程$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$(a>b>0),半焦距为c,
两焦点分别为F1,F1,运行中的航天员为P,
由已知可得:$\left\{\begin{array}{l}{{d}_{1}+R=a-c}\\{{d}_{2}+R=a+c}\end{array}\right.$,则2a=d1+d2+2R,
神秘信号的最短距离为丨PF1丨+丨PF2丨-2R=2a-2R=d1+d2,
神秘信号传导的最短距离d1+d2,
故选D.
点评 本题考查椭圆的性质,考查椭圆定义的物理应用,考查利用椭圆方程解决实际问题的能力,属于中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
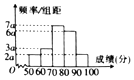 已知在一次全国数学竞赛中,某市3000名参赛学生的初赛成绩统计如图所示.
已知在一次全国数学竞赛中,某市3000名参赛学生的初赛成绩统计如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$+$\frac{1}{2}$i | B. | $\frac{1}{2}$-$\frac{1}{2}$i | C. | $\frac{1}{2}$i | D. | -$\frac{1}{2}$i |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 30° | B. | 60° | C. | 150° | D. | 120° |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在多面体ABCDEF中,底面ABCD是边长为2的菱形,∠BAD=60°,四边形BDEF是矩形,平面BDEF⊥平面ABCD,DE=2,M为线段BF上一点,且DM⊥平面ACE.
如图,在多面体ABCDEF中,底面ABCD是边长为2的菱形,∠BAD=60°,四边形BDEF是矩形,平面BDEF⊥平面ABCD,DE=2,M为线段BF上一点,且DM⊥平面ACE.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com