
分析 (Ⅰ)由题意可知a=2b2,a2-b2=c2=3,即可求得a和b的值,求得椭圆方程;
(Ⅱ)由4y1y2=x1x2,当直线AB的斜率存在且不为0时,设直线方程为y=kx+m,代入椭圆方程,利用根与系数的关系求得A,B的横坐标的和与积,结合4y1y2=x1x2,求得k,把三角形AOB的面积化为关于m的函数,利用基本不等式求其最值,进一步得到四边形ABCD面积的最大值.
解答 解:(Ⅰ)由题意可知:PF垂直于x轴,则c=$\sqrt{3}$,$\frac{{b}^{2}}{a}$=$\frac{1}{2}$,即a=2b2,
a2-b2=c2=3,
则a=2,b=1,
∴椭圆的标准方程:$\frac{{x}^{2}}{4}+{y}^{2}=1$;
(Ⅱ)∵$\frac{{{y}_{1}y}_{2}}{\overrightarrow{OA}•\overrightarrow{OB}}$=$\frac{1}{5}$,4y1y2=x1x2,
若直线AB的斜率不存在(或AB的斜率为0时),不满足4y1y2=x1x2;
直线AB的斜率存在且不为0时,设直线方程为y=kx+m,A(x1,y1),B(x2,y2).
联立$\left\{\begin{array}{l}{y=kx+m}\\{\frac{{x}^{2}}{4}+{y}^{2}=1}\end{array}\right.$,得(1+4k2)x2+8kmx+4(m2-1)=0.
△=(8km)2-4(1+4k2)(4m2-4)=16(4k2-m2+1)>0,①
x1+x2=-$\frac{8km}{1+4{k}^{2}}$,x1x2=$\frac{4({m}^{2}-1)}{1+4{k}^{2}}$.
∵4y1y2=x1x2,又y1y2=(kx1+m)(kx2+m)=k2x1x2+km(x1+x2)+m2,
∴(4k2-1)x1x2+4km(x1+x2)+4m2=0,
即(4k2-1)$\frac{4({m}^{2}-1)}{1+4{k}^{2}}$+4km(-$\frac{8km}{1+4{k}^{2}}$)+4m2=0.
整理得:k=±$\frac{1}{2}$.
∵A、B、C、D的位置可以轮换,
∴AB、BC的斜率一个是$\frac{1}{2}$,另一个就是-$\frac{1}{2}$.
∴kAB+kBC=$\frac{1}{2}$-$\frac{1}{2}$=0,是定值.
不妨设kAB=-$\frac{1}{2}$,则x1+x2=2m,x1x2=2(m2-1).
设原点到直线AB的距离为d,则S△AOB=$\frac{1}{2}$|AB|•d=$\frac{1}{2}$|x1-x2|•$\frac{丨m丨}{\sqrt{1+{k}^{2}}}$
=$\frac{丨m丨}{2}$$\sqrt{({x}_{1}{+x}_{2})^{2}-4{x}_{1}{x}_{2}}$=$\sqrt{{m}^{2}(2-{m}^{2})}$≤1.
当m2=1时满足①取等号.
∴S四边形ABCD=4S△AOB≤4,即四边形ABCD面积的最大值为4.
∴四边形ABCD面积的最大值为4.
点评 本题考查椭圆的标准方程及简单几何性质,直线与椭圆的位置关系,考查韦达定理,直线的斜率公式,三角形的面积公式,考查计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 甲品牌1个,乙品牌8个 | B. | 甲品牌2个,乙品牌7个 | ||
| C. | 甲品牌3个,乙品牌6个 | D. | 甲品牌4个,乙品牌5个 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
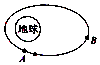 神舟五号飞船成功完成了第一次载人航天飞行,实现了中国人民的航天梦想,某段时间飞船在太空中运行的轨道是一个椭圆,地球在椭圆的一个焦点上,如图所示,假设航天员到地球最近距离为d1,到地球最远距离为d2,地球的半径为R,我们想象存在一个镜像地球,其中心在神舟飞船运行轨道的另外一个焦点上,上面住着一个神仙发射某种神秘信号需要飞行中的航天员中转后地球人才能接收到,则神秘信号传导的最短距离为( )
神舟五号飞船成功完成了第一次载人航天飞行,实现了中国人民的航天梦想,某段时间飞船在太空中运行的轨道是一个椭圆,地球在椭圆的一个焦点上,如图所示,假设航天员到地球最近距离为d1,到地球最远距离为d2,地球的半径为R,我们想象存在一个镜像地球,其中心在神舟飞船运行轨道的另外一个焦点上,上面住着一个神仙发射某种神秘信号需要飞行中的航天员中转后地球人才能接收到,则神秘信号传导的最短距离为( )| A. | d1+d2+R | B. | d2-d1+2R | C. | d2+d1-2R | D. | d1+d2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {0,1,2,4} | B. | {2,3} | C. | {2,4} | D. | {0,4} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com