练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    18．现从甲、乙两个品牌共9个不同的空气净化器中选出3个分别测试A、B、C三项指标，若取出的3个空气净化器中既有甲品牌又有乙品牌的概率为$\frac{5}{6}$，那么9个空气净化器中甲、乙品牌个数分布可能是（　　）
    A．甲品牌1个，乙品牌8个B．甲品牌2个，乙品牌7个
    C．甲品牌3个，乙品牌6个D．甲品牌4个，乙品牌5个

    分析 设9个空气净化器中甲、乙品牌个数分别为x，9-x.$\frac{{∁}_{x}^{1}{∁}_{9-x}^{2}+{∁}_{x}^{2}{∁}_{9-x}^{1}}{{∁}_{9}^{3}}$=$\frac{5}{6}$，化简解出即可得出．

    解答 解：设9个空气净化器中甲、乙品牌个数分别为x，9-x．
    $\frac{{∁}_{x}^{1}{∁}_{9-x}^{2}+{∁}_{x}^{2}{∁}_{9-x}^{1}}{{∁}_{9}^{3}}$=$\frac{5}{6}$，化为：x（8-x）（9-x）+x（x-1）（9-x）=7×5×4，化为x（9-x）=20，
    解得x=5或4．
    因此9个空气净化器中甲、乙品牌个数分别为5，4；或4，5．
    只有D有可能．
    故选：D．

    点评 本题考查了排列组合的计算公式、古典概率计算公式，考查了推理能力与计算能力，属于中档题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

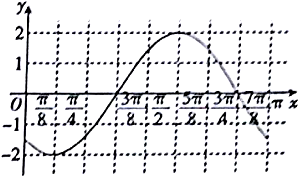    8．函数f（x）=Asin（ωx+φ）（ω＞0，$|φ|＜\frac{π}{2}$）的部分图象如图所示，将函数f（x）的图象向右平移$\frac{7π}{24}$个单位后得到函数g（x）的图象，若函数g（x）在区间$[{-\frac{π}{3}，θ}]$（$θ＞-\frac{π}{3}$）上的值域为[-1，2]，则θ=$\frac{π}{4}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    9．公差不为零的等差数列{an}的前n项和为Sn．若a4是a3与a7的等比中项，S8=16，则S10等于（　　）
    A．18B．24C．30D．60

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    6．已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1（a＞0，b＞0）$与抛物线y2=8x有一个公共的焦点F．设这两曲线的一个交点为P，若|PF|=5，则点P的横坐标是3；该双曲线的渐近线方程为y=±$\sqrt{3}$x．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    13．在平面直角坐标系xOy中．点M不与点O重合，称射线OM与圆x2+y2=1的交点N为点M的“中心投影点“．
    （1）点M（1，$\sqrt{3}$）的“中心投影点”为（$\frac{1}{2}$，$\frac{\sqrt{3}}{2}$）
    （2）曲线x2$-\frac{{y}^{2}}{3}=1$上所有点的“中心投影点”构成的曲线的长度是$\frac{4π}{3}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    3．企业需为员工缴纳社会保险，缴费标准是根据职工本人上一年度月平均工资（单位：元）的8%缴纳，某企业员工甲在2010年至2016年各年中每月所缴纳的养老保险数额y（单位：元）与年份序号t的统计如表：
     年份 20102011 2012 2013 2014 2015 2016 
     t 1 2 3 4 5 6 7
     y 270 330 390 450 490 540 610
    （1）求y关于t的线性回归方程$\widehat{y}$=$\widehat{b}$t+$\widehat{a}$；
    （2）按照这种变化趋势，利用（1）中回归方程，预测2017年该员工每月的平均工资（精确到0.1）．
    参考公式和数据：$\widehat{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{xy}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$，$\widehat{a}$=$\overline{y}$-b$\overline{x}$，$\sum_{i=1}^{7}$tiyi=13860，$\sum_{i=1}^{7}$ti2=140．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    10．设{an}是由正数组成的等比数列，Sn是{an}的前n项和．已知a2a4=16，S3=28，则a1a2…an最大时，n的值为3或4．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    7．已知点P（$\sqrt{3}$，$\frac{1}{2}$）在椭圆E：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）上，F为右焦点，PF垂直于x轴，A，B，C，D为椭圆上四个动点，且AC，BD交于原点O．
    （Ⅰ）求椭圆E的方程；
    （Ⅱ）设A（x1，y1），B（x2，y2），满足$\frac{{{y}_{1}y}_{2}}{\overrightarrow{OA}•\overrightarrow{OB}}$=$\frac{1}{5}$，判断kAB+kBC的值是否为定值，若是，求出此定值，并求出四边形ABCD面积的最大值，否则请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    8．某校高三年级某班的数学课外活动小组有6名男生，4名女生，从中选出4人参加数学竞赛考试，用X表示其中男生的人数．
    （Ⅰ）请列出X的分布列并求数学期望；
    （Ⅱ）根据所列的分布列求选出的4人中至少有3名男生的概率．

    查看答案和解析>>

    同步练习册答案