
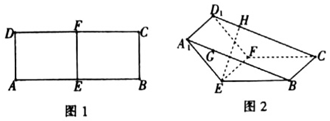
 如图1,在矩形ABCD中,AB=8,AD=3,点E、F分别为AB、CD的中点,将四边形AEFD沿EF折到A1EFD1的位置,使∠A1EB=120°,如图2所示,点G,H分别在A1B,D1C上,A1G=D1H=$\sqrt{3}$,过点G,H的平面α与几何体A1EB-D1FC的面相交,交线围成一个正方形.
如图1,在矩形ABCD中,AB=8,AD=3,点E、F分别为AB、CD的中点,将四边形AEFD沿EF折到A1EFD1的位置,使∠A1EB=120°,如图2所示,点G,H分别在A1B,D1C上,A1G=D1H=$\sqrt{3}$,过点G,H的平面α与几何体A1EB-D1FC的面相交,交线围成一个正方形.分析 (1)在BE或A1•E上取一点M,使得GM=GH=3,求出M点的位置即可作出截面图形;
(2)过E作出截面α的垂线,作出要求角,在直角三角形中计算余弦值.
解答 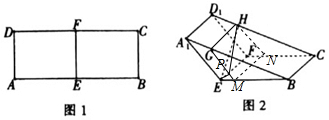 解:(1)由题意可知A1E=BE=4,GH=A1D1=3,
解:(1)由题意可知A1E=BE=4,GH=A1D1=3,
在△A1BE中,由余弦定理得A1B=$\sqrt{{4}^{2}+{4}^{2}-2×4×4×cos120°}$=4$\sqrt{3}$,
设平面α与几何体的截面正方形为GHNM,则GM=3,
若M在棱BE上,设BM=x,则由余弦定理得cos30°=$\frac{(3\sqrt{3})^{2}+{x}^{2}-9}{2•3\sqrt{3}•x}$=$\frac{\sqrt{3}}{2}$,解得x=3,
若M在棱A1E上,设A1M=x,则由余弦定理得cos30°=$\frac{3+{x}^{2}-9}{2•\sqrt{3}•x}$=$\frac{\sqrt{3}}{2}$,解得x=9(舍).
过M作MN∥EF交CF于N,连接GH,MN,GM,HN,
则正方形GHNM即为要作的正方形.
(2)过E作EP⊥GM,垂足为P,连接HP,
∵EF⊥A1E,EF⊥BE,A1E∩BE=E,
∴EF⊥平面A1BE,
∵A1G=D1H,∴GH∥EF,
∴GH⊥平面A1BE,又EP?平面A1BE,
∴EP⊥GH,又GH∩GM=G,GH?平面GHNM,GM?平面GHNM,
∴EP⊥平面GHNM,
∴∠EHP为直线EH与平面α所成的角,
由(1)可知GM∥A1E,EM=1,
∴∠PEM=30°,∴PM=$\frac{1}{2}$,PE=$\frac{\sqrt{3}}{2}$,
∴GP=$\frac{5}{2}$,PH=$\sqrt{{3}^{2}+(\frac{5}{2})^{2}}$=$\frac{\sqrt{61}}{2}$,EH=$\sqrt{P{H}^{2}+P{E}^{2}}$=4,
∴cos∠EHP=$\frac{PH}{EH}$=$\frac{\sqrt{61}}{8}$.
∴直线EH与平面α所成角的余弦值为$\frac{\sqrt{61}}{8}$.
点评 本题考查了线面平行的性质,线面角的计算,属于中档题.


 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
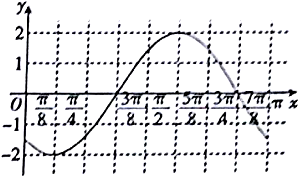 函数f(x)=Asin(ωx+φ)(ω>0,$|φ|<\frac{π}{2}$)的部分图象如图所示,将函数f(x)的图象向右平移$\frac{7π}{24}$个单位后得到函数g(x)的图象,若函数g(x)在区间$[{-\frac{π}{3},θ}]$($θ>-\frac{π}{3}$)上的值域为[-1,2],则θ=$\frac{π}{4}$.
函数f(x)=Asin(ωx+φ)(ω>0,$|φ|<\frac{π}{2}$)的部分图象如图所示,将函数f(x)的图象向右平移$\frac{7π}{24}$个单位后得到函数g(x)的图象,若函数g(x)在区间$[{-\frac{π}{3},θ}]$($θ>-\frac{π}{3}$)上的值域为[-1,2],则θ=$\frac{π}{4}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
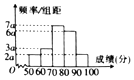 已知在一次全国数学竞赛中,某市3000名参赛学生的初赛成绩统计如图所示.
已知在一次全国数学竞赛中,某市3000名参赛学生的初赛成绩统计如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 18 | B. | 24 | C. | 30 | D. | 60 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com