
分析 (Ⅰ)函数整理为g(x)=alnx+2x,求导,由题意可知,函数的最小值应在极值点处取得,令f′(x)=0,代入求解即可;
(Ⅱ)函数整理为h(x)=alnx+ax2+(a2+2)x,求导得h′(x),对参数a进行分类讨论,逐一求出单调区间;
(Ⅲ)设出公共点坐标P(m,n)的坐标,求出坐标间的关系,得到lnm-m+1=0,通过讨论函数ω(x)=lnm-m+1的单调性解方程即可.
解答 解:(Ⅰ)g(x)=f(x)+2x=alnx+2x,(x>0),
g′(x)=$\frac{a}{x}$+2,
a≥0时,g′(x)>0,函数在(0,+∞)递增,无最小值,
a<0时,g′(x)=$\frac{a+2x}{x}$,令g′(x)>0,解得:x>-$\frac{a}{2}$,令g′(x)<0,解得:0<x<-$\frac{a}{2}$,
∴函数g(x)=f(x)+2x在(0,-$\frac{a}{2}$)递减,在(-$\frac{a}{2}$,+∞)递增,
故函数在x=-$\frac{a}{2}$处取得最小值,
∴aln(-$\frac{a}{2}$)-a=0,解得:a=-2e;
(Ⅱ)h(x)=f(x)+ax2+(a2+2)x
=alnx+ax2+(a2+2)x,
∴h′(x)=$\frac{(ax+1)(2x+a)}{x}$,
当a=0时,h(x)=2x,定义域内递增;
当a≠0时,
令h′(x)=0,∴x=-$\frac{1}{a}$或x=-$\frac{a}{2}$,
当a>0时,h′(x)>0,h(x)定义域内递增;
当a<0时,当a>-$\sqrt{2}$时,函数的增区间为(0,-$\frac{a}{2}$),(-$\frac{1}{a}$,+∞),减区间为(-$\frac{a}{2}$,-$\frac{1}{a}$);
当a<-$\sqrt{2}$时,函数的增区间为(0,-$\frac{1}{a}$),(-$\frac{a}{2}$,+∞),减区间为(-$\frac{1}{a}$,-$\frac{a}{2}$);
当a=-$\sqrt{2}$时,定义域内递增.
(Ⅲ)a=$\frac{1}{2}$符合题意,理由如下:此时P(1,0)
设函数f(x)与u(x)上公共点P(m,n),
依题意有f(m)=u(m),f′(m)=u′(m),
即$\frac{a}{m}=\frac{1}{2{m}^{2}}$,$\frac{m-1}{2m}=alnm$⇒得到lnm-m+1=0,构造函数ω(x)=lnm-m+1,(x>0)
ω′(x)=$\frac{1}{m}-1$,可得函数ω(x)在(0,1)递增,在(1,+∞)递减,而ω(1)=0
∴方程lnm-m+1=0有唯一解,即m=1,a=$\frac{1}{2}$
点评 本题考查了利用导函数求函数的单调性问题,难点是对导函数中参数的讨论问题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2014 | B. | -2015 | C. | -2016 | D. | -2017 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
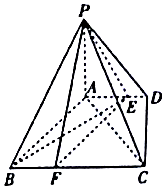 如图,四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD是直角梯形,∠ADC=90°,AD∥BC,AB⊥AC,AB=AC=$\sqrt{2}$,点E在AD上,且AE=2ED.
如图,四棱锥P-ABCD中,PA⊥底面ABCD,底面ABCD是直角梯形,∠ADC=90°,AD∥BC,AB⊥AC,AB=AC=$\sqrt{2}$,点E在AD上,且AE=2ED.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
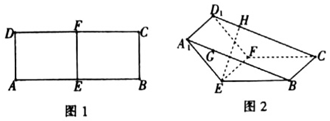 如图1,在矩形ABCD中,AB=8,AD=3,点E、F分别为AB、CD的中点,将四边形AEFD沿EF折到A1EFD1的位置,使∠A1EB=120°,如图2所示,点G,H分别在A1B,D1C上,A1G=D1H=$\sqrt{3}$,过点G,H的平面α与几何体A1EB-D1FC的面相交,交线围成一个正方形.
如图1,在矩形ABCD中,AB=8,AD=3,点E、F分别为AB、CD的中点,将四边形AEFD沿EF折到A1EFD1的位置,使∠A1EB=120°,如图2所示,点G,H分别在A1B,D1C上,A1G=D1H=$\sqrt{3}$,过点G,H的平面α与几何体A1EB-D1FC的面相交,交线围成一个正方形.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 8 | B. | 10 | C. | 12 | D. | 16 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | $\frac{2}{3}$ | C. | -1 | D. | $\frac{1}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com