
分析 (Ⅰ)化简函数f(x)=|x+1|+|x-a|(a>0)为分段函数,然后通过不等式f(x)≥5的解集为{x|x≤-2或x≥3},求a的值;
(Ⅱ)利用“1”的代换,利用基本不等式转化证明即可.
解答 (本小题满分10分)
解:(Ⅰ) 因为a>0,所以$f(x)=|x+1|+|x-a|=\left\{\begin{array}{l}-2x+a-1,x<-1\\ a+1,-1≤x<a\\ 2x-a+1,x≥a\end{array}\right.$,
又因为不等式f(x)≥5的解集为{x|x≤-2或x≥3},就是x=-2或x=3时,f(x)=5,解得a=2.(5分)
(Ⅱ)证明:$\frac{1}{a+b}+\frac{1}{b+c}+\frac{1}{c+a}=\frac{{(\frac{1}{a+b}+\frac{1}{b+c}+\frac{1}{c+a})(a+b+b+c+c+a)}}{2m}$
=$\frac{{1+\frac{b+c}{a+b}+\frac{c+a}{a+b}+1+\frac{a+b}{b+c}+\frac{c+a}{b+c}+1+\frac{a+b}{c+a}+\frac{b+c}{c+a}}}{2m}$
=$\frac{{3+\frac{b+c}{a+b}+\frac{a+b}{b+c}+\frac{c+a}{b+c}+\frac{b+c}{c+a}+\frac{a+b}{c+a}+\frac{c+a}{a+b}}}{2m}≥\frac{9}{2m}$(10分)
点评 本小题主要考查含绝对值不等式以及不等式证明的相关知识,本小题重点考查考生的化归与转化思想.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-1,+∞) | B. | (-1,+∞) | C. | [-$\frac{1}{2}$,+∞) | D. | R |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 秦九韶是我国南宋时期的数学家,他在《数学九章》中提出的多项式的秦九韶算法,至今仍是比较先进的算法,如图是事项该算法的程序框图,执行该程序框图,若输入n,x的值分别为4,2,则输出v的值为( )
秦九韶是我国南宋时期的数学家,他在《数学九章》中提出的多项式的秦九韶算法,至今仍是比较先进的算法,如图是事项该算法的程序框图,执行该程序框图,若输入n,x的值分别为4,2,则输出v的值为( )| A. | 5 | B. | 12 | C. | 25 | D. | 50 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
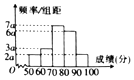 已知在一次全国数学竞赛中,某市3000名参赛学生的初赛成绩统计如图所示.
已知在一次全国数学竞赛中,某市3000名参赛学生的初赛成绩统计如图所示.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com